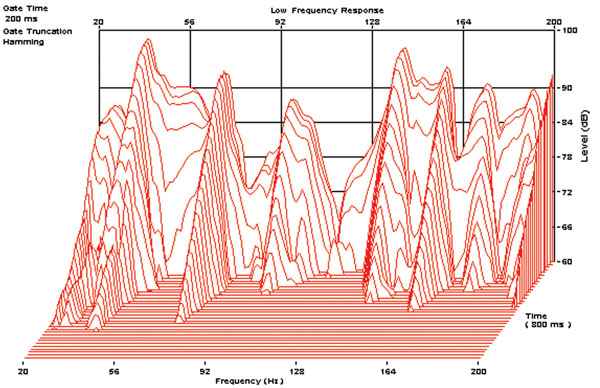
Fig. 1 Low frequency measurement in a typical listening room.
As stated in my earlier article (How do listening room acoustics affect sound quality?), room modes cause standing waves that can cause three acoustical problems: a level boost at some frequencies, an extent of the duration of sound at those same frequencies (resonance) and some profound dips at other frequencies.
These acoustical phenomena can produce resonant bass sound that has holes in it and suffers a lack of tightness. The subwoofer’s frequency response will be greatly affected, and it should be noted that standing wave problems can extend up to about 300 Hz.
Figure 1 shows a low frequency measurement in a typical listening room. On the amplitude scale (the Y axis, labelled “level”), we can see a very irregular response. The time scale (the Z axis, labelled “time”) is also very important. We can see that the resonances last a certain time. Some call this ringing. (Other rooms could easily exhibit longer ringing time.)
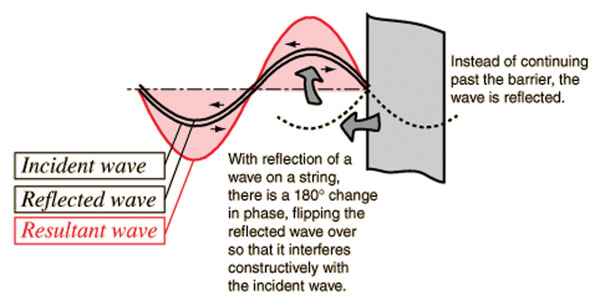Fig. 2 The reflected wave adds to the incident one.
The standing wave
Have you ever sung in a bathroom? Some notes seem to make the whole room resonate. In fact, this is exactly what happens. The note that you are singing is probably one of the room’s standing waves. A standing wave is a low frequency resonance that takes place between two opposite walls as the reflected wave interferes constructively with the incident wave. The resonant frequency depends on the distance between the two walls.
There will be many room modes between two walls as the phenomenon will repeat itself at multiples of the first frequency: 2f, 3f, etc.
Standing waves pressure in a room
Let’s take a room which has two walls that are 10 feet apart. Between those two walls, there will be room modes at: f=56 Hz, 2f=112 Hz, 3f=168 Hz etc…
One can note that:
• The sound pressure level is not equal in the room
• The first resonance has near 0 SPL (sound pressure level) at the centre of the space, the same for its odd multiples
• The even multiples have maximum SPL at the center
• All room modes have maximum SPL near the walls
This explains why the low frequency response changes as we change the listening spot in a room. It also explains why we have so much bass close to a wall.
Since there are three dimensions in a room, there will be three series of room modes.
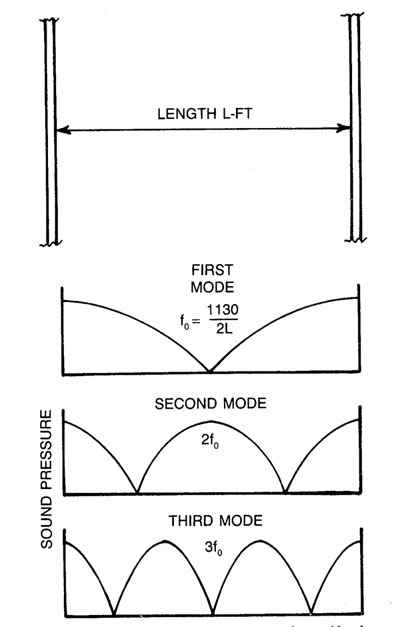Fig. 3 Distribution of the standing waves sound pressure level between two walls.
How to solve the problem?
The phenomenon is unavoidable; there are standing waves even in the best rooms. How to minimize the problem? One way is to distribute those frequencies in the spectrum so that they won’t be too close to each other; otherwise they can add up, if they are at high amplitude at the same place in the room, namely the listening spot. What’s more, they must not be too far away from each other because there can be an audible ” hole ” created in the frequency response. This is a rule applied even if we know that there will be holes in the frequency response, since all room modes are not heard at a single spot.
Influential factors to get a good distribution of those resonant frequencies are the volume of the room and its dimension ratio. Gilford1 states that the axial modes spacing should not be less than 5 Hz and not more than 20 Hz.
In smaller rooms, the Davis2 frequency marks the superior limit from which modal density becomes high enough so there won’t be any colouration due to standing waves;
This rule is highly approximate. In an average size listening room, this frequency is around 350 to 450 Hz. The larger the smallest dimension, the lower this frequency is and, usually, the fewer problems we have.
Room analysis
Axial modes are issued from reflections on two surfaces. There are also tangential and oblique modes, which will be discussed later. Axial mode analysis makes it possible to identify the problems and to optimise the dimensions of the room in order to get a better axial modes distribution. Here is a tool to do such an analysis:
www.hometheatershack.com/roomcalculator.xls
This calculator is used in the upcoming part of the article.
Large room or small room?
Here are two rooms of different volumes with the same ratio of dimensions.
Using the calculator, when we enter the dimensions of the smaller room, we can see that there are several gaps of more than 20 Hz between modes. (see figure 4)
These “holes” can bring some colouration in the low frequency response. This is because smaller dimensions give higher frequencies, thus larger gaps between them. The situation is typical of small rooms and cannot be avoided. The same exercise done with the dimensions of the larger room shows less of such problems. (see figure 5 on the next page)
In general, the minimum volume I recommend for a listening room is around 1500 to 2000 cu ft.
Axial analysis and correction of a typical room
Let us take a typical room for which a reader asked for advice; 8′ x 11.75′ x 18′ (2.44m x 3.6m x 5.5m). Room proportions 1 :1.47 :2.25 are very close to one reported by Louden3 as being good; 1 :1.5 :2.20. Nevertheless, there will be three potential problems. By using the same tool as before (see figure 6), we can see that three pairs of modes may be problematic since their frequencies are too close to each other. (See also table 3)
Changing one or two dimensions can solve the situation. To do this, we must determine which frequency belongs to which dimension. A table like the one in the calculator is necessary.
In table 4, one can note that the problematic frequencies of 96 Hz, 144 Hz and 192 Hz are all related to the width. Those three frequencies should be a little bit higher to widen the gap between their precedents. If the width is slightly diminished (enter 11.33′ instead of 11.75′), the three problems have disappeared (see figure 7).
Were those three frequencies a real problem?
First, let’s say that the listening spot in this room is exactly in the middle. For the first conflict, 94 Hz is of the third order (odd multiple) (see table 4) and 96 Hz is of the second order (even multiple). So being of “opposite” amplitudes, they will not add up. The same for 141 and 144 Hz. On the contrary, 188 and 192 Hz could add together since they both are even multiples, that is at maximum pressure level at the center of the room.
Michel Leduc is an acoustics professor (Cégep of Drummondville), researcher (Musilab, CCTT sound technologies) and acoustical consultant (Sonart Acoustique, www.sonartacoustique.com). He can be contacted by email at
info@sonartacoustique.com.
About the Author: admin
GreenGoogle
[…]that will be the finish of this report. Right here youll discover some web sites that we assume youll value, just click the hyperlinks over[…]
Scottsdale Nail Salon
[…]always a significant fan of linking to bloggers that I adore but do not get a whole lot of link adore from[…]
best masturbation toys
[…]here are some hyperlinks to internet sites that we link to for the reason that we feel they’re worth visiting[…]
luxury vibrator
[…]below youll obtain the link to some sites that we think you must visit[…]
guitar scales
[…]although websites we backlink to beneath are considerably not associated to ours, we feel they may be essentially really worth a go by, so have a look[…]
Third Party Manufacturing In West Bengal
[…]Here are several of the websites we suggest for our visitors[…]
Best penis pumps
[…]Sites of interest we have a link to[…]
G spot vibrator review
[…]although web sites we backlink to beneath are considerably not related to ours, we feel they are in fact worth a go by way of, so possess a look[…]
Porometria Apunte
[…]here are some hyperlinks to web pages that we link to mainly because we think they’re worth visiting[…]
Week 8 Reflections for week 8 rubric etc – Learning and Communicating Online
[…]Here is an excellent Blog You might Uncover Interesting that we Encourage You[…]
TEMA. 2 Apunte
[…]Here are a few of the web pages we recommend for our visitors[…]
Agen judi Online
[…]please stop by the websites we adhere to, like this 1, because it represents our picks in the web[…]
Best anal vibrators
[…]we like to honor numerous other internet websites on the internet, even though they arent linked to us, by linking to them. Beneath are some webpages worth checking out[…]
5 – Resumen University Physics with Modern Physics
[…]that would be the finish of this write-up. Right here youll locate some web pages that we feel you will value, just click the hyperlinks over[…]
Vouchers for shopping
[…]we came across a cool web-site which you could take pleasure in. Take a look when you want[…]
g spot vibrator
[…]very few websites that transpire to become detailed below, from our point of view are undoubtedly nicely worth checking out[…]
flexible vibrator
[…]we prefer to honor several other online web sites on the net, even if they arent linked to us, by linking to them. Under are some webpages worth checking out[…]
Cheap FUT Coins
[…]that is the finish of this report. Here you will find some websites that we assume you will appreciate, just click the hyperlinks over[…]
wand massager
[…]always a big fan of linking to bloggers that I appreciate but do not get quite a bit of link really like from[…]
Chicago SEO
[…]Sites of interest we’ve a link to[…]
detox tea
[…]we came across a cool site that you just may take pleasure in. Take a look if you want[…]
Social Media Marketing Company in Karachi
[…]The info mentioned inside the report are a number of the most beneficial obtainable […]
magic massager
[…]check below, are some totally unrelated web sites to ours, however, they are most trustworthy sources that we use[…]
the curve body massager
[…]below you will find the link to some web-sites that we consider you must visit[…]
thrusting rabbit
[…]check beneath, are some entirely unrelated internet sites to ours, nonetheless, they are most trustworthy sources that we use[…]
chwilówki
[…]just beneath, are a lot of entirely not connected websites to ours, however, they are certainly really worth going over[…]
phone screen repair
[…]Here are several of the web sites we advocate for our visitors[…]
cyberskin extension
[…]below you will find the link to some internet sites that we believe it is best to visit[…]
american bombshell big boy
[…]that could be the finish of this post. Here you will discover some sites that we consider youll appreciate, just click the links over[…]
evolved sex toy
[…]Here are several of the web sites we suggest for our visitors[…]
anal vibrator
[…]that may be the end of this post. Right here youll locate some sites that we assume youll value, just click the hyperlinks over[…]
Porn City XXX
[…]we like to honor lots of other net web-sites on the net, even though they arent linked to us, by linking to them. Beneath are some webpages really worth checking out[…]
suction cup dong
[…]just beneath, are various completely not connected web sites to ours, having said that, they are surely really worth going over[…]
mail order bride
[…]The facts mentioned inside the article are a few of the top out there […]
detroit seo
[…]one of our guests not too long ago recommended the following website[…]
Lawn
[…]we like to honor a lot of other online sites around the net, even when they arent linked to us, by linking to them. Beneath are some webpages worth checking out[…]
male enhancement pump
[…]here are some hyperlinks to web pages that we link to simply because we consider they may be worth visiting[…]
vibrating pleasure balls
[…]we came across a cool site which you could possibly delight in. Take a look should you want[…]
anal butt plug
[…]below you will come across the link to some web sites that we believe you must visit[…]
vibrating dildo
[…]usually posts some quite interesting stuff like this. If youre new to this site[…]
188bet
[…]we came across a cool internet site that you may take pleasure in. Take a search when you want[…]
free download for windows 7
[…]please take a look at the internet sites we follow, like this a single, because it represents our picks from the web[…]
free download for windows 8
[…]Here is a great Blog You may Locate Exciting that we Encourage You[…]
apps download for windows 7
[…]just beneath, are various completely not related web-sites to ours, having said that, they may be certainly worth going over[…]
apps download for windows 7
[…]check beneath, are some entirely unrelated internet websites to ours, however, they’re most trustworthy sources that we use[…]
chevrolet dealer houston tx
[…]Here are a number of the web pages we suggest for our visitors[…]
sexy gatas na web
[…]the time to study or take a look at the content material or internet sites we have linked to below the[…]
toy rabbit
[…]Every as soon as in a when we pick out blogs that we study. Listed below would be the newest sites that we select […]
best butt plug
[…]check beneath, are some completely unrelated web-sites to ours, nevertheless, they’re most trustworthy sources that we use[…]
Bella Aurora vergelijken
[…]Sites of interest we have a link to[…]
best stroker for men
[…]here are some hyperlinks to sites that we link to for the reason that we consider they’re worth visiting[…]
Speelgoedwatersproeier prijs
[…]check below, are some completely unrelated internet websites to ours, on the other hand, they are most trustworthy sources that we use[…]
pc app free download
[…]we prefer to honor lots of other world-wide-web web-sites around the web, even if they arent linked to us, by linking to them. Beneath are some webpages worth checking out[…]
free download for windows 8
[…]we came across a cool internet site which you may well love. Take a search in case you want[…]
apps for pc download
[…]always a big fan of linking to bloggers that I like but do not get a whole lot of link really like from[…]
silicone bullet vibrator
[…]below you will discover the link to some sites that we think you need to visit[…]
testicle ring
[…]Every once inside a though we pick out blogs that we study. Listed beneath are the most current internet sites that we opt for […]
app download for pc
[…]one of our visitors recently proposed the following website[…]
Gurgaon
[…]Sites of interest we’ve a link to[…]
dani daniels videos
[…]Sites of interest we’ve a link to[…]
vibrating wand massager
[…]the time to study or take a look at the content material or web-sites we’ve linked to below the[…]
Bàn làm việc
[…]we came across a cool internet site that you simply may well take pleasure in. Take a appear if you want[…]
shemale sexdate
[…]that may be the end of this article. Here you will come across some internet sites that we feel youll appreciate, just click the links over[…]
rencontres sexe
[…]one of our guests not too long ago encouraged the following website[…]
male p spot massager
[…]Every after in a while we pick out blogs that we study. Listed beneath would be the newest sites that we pick out […]
butt plug
[…]just beneath, are several entirely not related web-sites to ours, however, they are surely worth going over[…]
dv56h9100gg/a2
[…]The info talked about within the report are a number of the most beneficial out there […]
adult toys
[…]very few internet websites that occur to be comprehensive beneath, from our point of view are undoubtedly nicely really worth checking out[…]
https://opencollective.com/oneworldherald/
[…]very handful of websites that transpire to become comprehensive below, from our point of view are undoubtedly very well really worth checking out[…]
huge dildo
[…]although internet sites we backlink to below are considerably not associated to ours, we feel they’re truly really worth a go by, so possess a look[…]
how to make penis bigger
[…]Here is a superb Blog You may Find Intriguing that we Encourage You[…]
double headed dildo
[…]usually posts some extremely exciting stuff like this. If you are new to this site[…]
anal trainer
[…]check below, are some absolutely unrelated websites to ours, even so, they are most trustworthy sources that we use[…]
Ghostwriter Agentur
[…]that is the finish of this write-up. Here youll find some internet sites that we assume you will enjoy, just click the hyperlinks over[…]
scrap cars removal abbotsford
[…]Wonderful story, reckoned we could combine a handful of unrelated data, nevertheless definitely worth taking a search, whoa did 1 study about Mid East has got far more problerms too […]
job testing video games
[…]one of our visitors not long ago recommended the following website[…]
li2323s
[…]usually posts some pretty exciting stuff like this. If youre new to this site[…]
тхор
[…]Sites of interest we have a link to[…]
adam and eve vibrator
[…]below you will locate the link to some web-sites that we believe you’ll want to visit[…]
anal sex gel
[…]below youll uncover the link to some web sites that we think you ought to visit[…]
adult board games
[…]one of our guests a short while ago recommended the following website[…]
how to use ben wa balls
[…]The details talked about in the post are a number of the most effective readily available […]
Anabolic Steroids
[…]the time to read or pay a visit to the material or internet sites we have linked to beneath the[…]
blockchain advisory
[…]one of our visitors recently proposed the following website[…]
satta king
[…]always a major fan of linking to bloggers that I love but dont get lots of link adore from[…]
female vibrator
[…]we came across a cool internet site that you could delight in. Take a search when you want[…]
realistic male stroker
[…]Every once inside a even though we select blogs that we read. Listed below would be the most up-to-date sites that we pick out […]
g spot vibrator review
[…]the time to read or pay a visit to the content or web-sites we have linked to below the[…]
bullet vibe
[…]that will be the end of this article. Here youll uncover some websites that we consider you will enjoy, just click the hyperlinks over[…]
adam and eve vibrating stroker
[…]please take a look at the internet sites we follow, like this 1, because it represents our picks from the web[…]
butt plugs for gays
[…]that will be the finish of this report. Right here youll discover some web pages that we believe you will value, just click the links over[…]
gay toy bondage
[…]Every after inside a while we opt for blogs that we study. Listed beneath are the newest web-sites that we pick out […]
pornland
[…]check below, are some entirely unrelated internet websites to ours, even so, they are most trustworthy sources that we use[…]
butterfly remote vibrator
[…]here are some hyperlinks to web sites that we link to for the reason that we consider they’re worth visiting[…]
https://harness4.com/best-climbing-tree-stand/
[…]below youll find the link to some web-sites that we feel you must visit[…]
best blow job tips
[…]we like to honor lots of other world-wide-web web-sites around the internet, even when they arent linked to us, by linking to them. Underneath are some webpages really worth checking out[…]
dslr camera
[…]very few web-sites that come about to become in depth below, from our point of view are undoubtedly properly worth checking out[…]
rubbish bin hire
[…]Every the moment inside a when we select blogs that we read. Listed beneath are the most up-to-date web pages that we select […]
SSRU
[…]Every once in a even though we opt for blogs that we read. Listed beneath are the newest web-sites that we decide on […]
top rabbit vibrators
[…]Sites of interest we’ve a link to[…]
best realistic dildo
[…]although internet sites we backlink to below are considerably not connected to ours, we feel they may be actually really worth a go by way of, so have a look[…]
bullet vibe
[…]Sites of interest we’ve a link to[…]
sex toys haul
[…]please check out the web-sites we adhere to, which includes this a single, because it represents our picks through the web[…]
bullet vibrator
[…]we like to honor many other web web pages on the internet, even if they arent linked to us, by linking to them. Beneath are some webpages worth checking out[…]
Driewieler
[…]please stop by the web sites we comply with, such as this 1, because it represents our picks from the web[…]
lingerie stocking
[…]Here is an excellent Weblog You may Find Fascinating that we Encourage You[…]
15% minoxidil
[…]Here is an excellent Weblog You might Locate Interesting that we Encourage You[…]
15% minoxidil
[…]Here is a good Blog You may Discover Intriguing that we Encourage You[…]
Julia Ann
[…]here are some hyperlinks to web pages that we link to simply because we assume they’re worth visiting[…]
bdjobs bd
[…]Here is a good Weblog You may Discover Interesting that we Encourage You[…]
Fashion Station
[…]Sites of interest we’ve a link to[…]
Pool Services
[…]just beneath, are various absolutely not associated sites to ours, nevertheless, they’re surely really worth going over[…]
porno files
[…]the time to read or pay a visit to the subject material or web-sites we’ve linked to below the[…]
pornofilmpjes
[…]that would be the end of this post. Here you will locate some web pages that we believe youll enjoy, just click the links over[…]
southbury ct plumbers
[…]we came across a cool web-site that you simply could enjoy. Take a appear if you want[…]
1_iptv.m3u
[…]we like to honor several other world-wide-web web-sites on the net, even though they arent linked to us, by linking to them. Underneath are some webpages really worth checking out[…]
suicide is painless перевод
[…]Every once in a whilst we select blogs that we read. Listed below would be the most recent web pages that we opt for […]
russian translation hello
[…]check below, are some absolutely unrelated internet sites to ours, however, they are most trustworthy sources that we use[…]
Fifty Shades of Grey The Pinch Adjustable Nipple Clamps
[…]Sites of interest we have a link to[…]
xvideos
[…]always a huge fan of linking to bloggers that I love but do not get quite a bit of link love from[…]
plus size corset
[…]The information talked about within the post are several of the most effective available […]
https://search.yahoo.com/search?p=porn+land+xxx&fr=yfp-t&fp=1&toggle=1&cop=mss&ei=UTF-8
[…]just beneath, are quite a few entirely not associated web-sites to ours, having said that, they’re surely worth going over[…]
مساج بالقاهرة مدربات
[…]below you will come across the link to some web sites that we consider you should visit[…]
hageorm hund
[…]just beneath, are various totally not connected web pages to ours, having said that, they’re certainly worth going over[…]
beautiful Arab women
[…]The info mentioned in the post are a number of the most beneficial out there […]
messagerie outlook
[…]usually posts some pretty interesting stuff like this. If you are new to this site[…]
bdsm bondage
[…]we prefer to honor numerous other world wide web websites around the web, even when they arent linked to us, by linking to them. Beneath are some webpages worth checking out[…]
rabbit vibrator
[…]Wonderful story, reckoned we could combine several unrelated information, nonetheless truly worth taking a appear, whoa did one discover about Mid East has got far more problerms also […]
podcast
[…]check below, are some entirely unrelated websites to ours, having said that, they may be most trustworthy sources that we use[…]
bullet vibrator
[…]very couple of web-sites that happen to become detailed beneath, from our point of view are undoubtedly nicely really worth checking out[…]
mens c ring
[…]Sites of interest we have a link to[…]
home decor quizzes
[…]here are some links to sites that we link to mainly because we think they’re worth visiting[…]
Ντετέκτιβ Θεσσαλονίκη
[…]Here are a number of the internet sites we suggest for our visitors[…]
buy binds cs go
singularity offers premium & free undetected csgo cheats with predefined configs that are updated frequently with 24/7 support.
AOL Mail Login
[…]the time to read or stop by the content or web pages we’ve linked to beneath the[…]
iCloud Login
[…]please stop by the web-sites we stick to, which includes this 1, as it represents our picks through the web[…]
Philadelphia Elibrary
Explore electronic resources for free, thousands of eBooks, accounting eBooks, business eBooks, Marketing eBooks, Accounting eBooks, Banking eBooks, Design eBooks, Customers eBooks, Travel and Tourism eBooks and more
save sea turtle bracelet
[…]here are some links to sites that we link to because we think they are worth visiting[…]
döner bestellen hamburg
[…]Wonderful story, reckoned we could combine some unrelated information, nonetheless definitely worth taking a search, whoa did one discover about Mid East has got extra problerms at the same time […]
sex toys for couples
[…]one of our visitors lately proposed the following website[…]
Ultras logo
[…]one of our visitors not long ago advised the following website[…]
cock ring for couples
[…]please check out the web sites we comply with, such as this one, as it represents our picks from the web[…]
doc johnson
[…]we like to honor quite a few other web websites around the net, even when they arent linked to us, by linking to them. Below are some webpages worth checking out[…]
iraniporn
[…]please take a look at the internet sites we adhere to, which includes this one, because it represents our picks in the web[…]
walmart1
[…]Here are a number of the web pages we recommend for our visitors[…]
websites
[…]please take a look at the web sites we stick to, which includes this 1, because it represents our picks from the web[…]
nigerian mp3
[…]that is the end of this article. Right here you will discover some web sites that we think youll appreciate, just click the links over[…]
PPPD-780
[…]below you will find the link to some web-sites that we feel you need to visit[…]
butt plugs
[…]The info talked about in the article are a few of the ideal obtainable […]
افلام نيك يدوي
[…]very few web-sites that occur to become detailed beneath, from our point of view are undoubtedly well really worth checking out[…]
Likes
[…]very handful of web sites that happen to become in depth below, from our point of view are undoubtedly properly really worth checking out[…]
Entertainment News in Ghana
[…]please stop by the internet sites we comply with, such as this one particular, because it represents our picks from the web[…]
best sex toys
[…]Sites of interest we have a link to[…]
anal douches
[…]we like to honor many other world-wide-web web sites around the internet, even though they arent linked to us, by linking to them. Below are some webpages really worth checking out[…]
http://www.prepaidgiftbalance.com register your card
[…]the time to read or pay a visit to the content material or web-sites we’ve linked to below the[…]
prepaidgiftbalance.com register
[…]Every the moment in a while we choose blogs that we read. Listed below are the most current websites that we opt for […]
sex irani
[…]the time to read or go to the material or web pages we’ve linked to beneath the[…]
blue dildo
[…]Every as soon as in a even though we pick out blogs that we study. Listed below would be the most current web pages that we pick […]
how to guitar solo
[…]Every as soon as inside a although we choose blogs that we read. Listed below would be the most recent web pages that we decide on […]
siofok siofok siofok siofok
[…]we came across a cool site which you might get pleasure from. Take a look should you want[…]
judi online terpercaya
[…]Here is a superb Blog You may Uncover Fascinating that we Encourage You[…]
free download for windows 8
[…]The facts mentioned in the post are several of the ideal available […]
pc games free download for windows
[…]one of our guests a short while ago recommended the following website[…]
free apps download for windows 10
[…]the time to study or visit the material or web-sites we have linked to beneath the[…]
pc games for windows 10
[…]very few websites that transpire to become in depth beneath, from our point of view are undoubtedly effectively really worth checking out[…]
pc games for windows 10
[…]below you will uncover the link to some web pages that we consider you’ll want to visit[…]
visa card buy
[…]Here are several of the web pages we advocate for our visitors[…]
full apps download
[…]one of our guests lately suggested the following website[…]
pc games full version download
[…]Here are a few of the websites we recommend for our visitors[…]
free download for windows 10
[…]the time to read or pay a visit to the content material or sites we’ve linked to beneath the[…]
free download for windows pc
[…]Here is an excellent Blog You may Locate Intriguing that we Encourage You[…]
Eweka
[…]that would be the end of this article. Right here you will find some web pages that we consider youll appreciate, just click the links over[…]
Minyak Kelapa
[…]one of our visitors recently recommended the following website[…]
how to give a bj
[…]the time to study or go to the subject material or websites we have linked to below the[…]
government student loans
[…]very couple of websites that transpire to be detailed below, from our point of view are undoubtedly nicely really worth checking out[…]
how to verify paypal account with virtual visa and mastercard.
[…]Sites of interest we have a link to[…]
vibrating bullet massager
[…]one of our guests not long ago advised the following website[…]
stiiizy pods
[…]Here are several of the sites we advocate for our visitors[…]
العاب طبخ
[…]always a significant fan of linking to bloggers that I like but dont get a lot of link really like from[…]
brass knuckles vape pen
[…]Sites of interest we’ve a link to[…]
Indian Family Lawyer
[…]check beneath, are some absolutely unrelated web sites to ours, nonetheless, they are most trustworthy sources that we use[…]
Dank Vapes Official
[…]here are some hyperlinks to internet sites that we link to because we think they are really worth visiting[…]
THC vape juice discreet shipping USA
[…]we came across a cool web-site which you may well take pleasure in. Take a search in case you want[…]
Modafinil Armodafinil
[…]the time to read or pay a visit to the material or websites we’ve linked to below the[…]
https://www.amazon.com/dp/B07W6SP89N/ref=sr_1_1?keywords=books+best+sellers&qid=1565320651&s=digital-text…
[…]The information and facts mentioned in the report are a number of the best out there […]
Mini Baccarat Strategy
[…]here are some hyperlinks to web pages that we link to since we consider they may be really worth visiting[…]
Golden Eagle Blackjack Strategy
[…]we prefer to honor many other internet internet sites on the web, even when they arent linked to us, by linking to them. Underneath are some webpages worth checking out[…]
Roulette Strategy
[…]we came across a cool website that you simply might love. Take a search if you want[…]
Cool t shirts
[…]Here is a good Blog You might Find Intriguing that we Encourage You[…]
Hotels & Clubs Cleaning Sydney
[…]The info mentioned in the write-up are a number of the best accessible […]
Ioe business
[…]Every once in a when we opt for blogs that we read. Listed below are the most recent web pages that we opt for […]
exotic carts flavors
[…]we prefer to honor quite a few other net web-sites on the web, even when they arent linked to us, by linking to them. Under are some webpages worth checking out[…]
free ads Canada
[…]just beneath, are various absolutely not related websites to ours, however, they are surely worth going over[…]
kingpen carts
[…]just beneath, are numerous entirely not associated web pages to ours, nevertheless, they may be certainly worth going over[…]
gay male sex toys
[…]Wonderful story, reckoned we could combine several unrelated information, nevertheless seriously worth taking a look, whoa did 1 master about Mid East has got much more problerms as well […]
best lube for sex
[…]very few internet websites that occur to be comprehensive beneath, from our point of view are undoubtedly nicely worth checking out[…]
web design agency
[…]below youll come across the link to some web sites that we assume you must visit[…]
IPX-363
[…]one of our guests recently advised the following website[…]
onewalmart
[…]one of our guests not long ago advised the following website[…]
سكس مترجم سحاق
[…]Here is an excellent Blog You may Locate Intriguing that we Encourage You[…]
anal cleansing
[…]the time to read or check out the content material or web sites we’ve linked to beneath the[…]
realistic dildo
[…]Wonderful story, reckoned we could combine a number of unrelated data, nonetheless really really worth taking a appear, whoa did 1 find out about Mid East has got extra problerms too […]
SEO Vancouver
[…]that may be the finish of this write-up. Right here you will locate some sites that we believe you will appreciate, just click the hyperlinks over[…]
https://findlocationsnearme.net/
[…]Wonderful story, reckoned we could combine several unrelated information, nonetheless truly worth taking a appear, whoa did one particular learn about Mid East has got extra problerms as well […]
https://newbizhelp.org/my-getresponse-review-heres-what-i-really-think/
[…]very handful of internet sites that take place to become detailed beneath, from our point of view are undoubtedly effectively really worth checking out[…]
PPPD-792
[…]just beneath, are a lot of entirely not related sites to ours, however, they are surely worth going over[…]
Mumbai Escorts
[…]Sites of interest we’ve a link to[…]
sex swing
[…]Here is an excellent Blog You might Discover Intriguing that we Encourage You[…]
bullet massager
[…]Every after inside a whilst we choose blogs that we study. Listed below would be the most recent websites that we pick out […]
pc games for windows xp
[…]just beneath, are numerous completely not connected sites to ours, nevertheless, they are surely really worth going over[…]
download free games
[…]Here is a great Weblog You may Discover Fascinating that we Encourage You[…]
pc app free download
[…]very handful of sites that occur to be comprehensive below, from our point of view are undoubtedly nicely really worth checking out[…]
app pc download for windows
[…]Wonderful story, reckoned we could combine some unrelated data, nonetheless definitely really worth taking a appear, whoa did one discover about Mid East has got more problerms too […]
online surveys and follow-up autoresponders
[…]very few sites that take place to become comprehensive below, from our point of view are undoubtedly nicely worth checking out[…]
crazybulk opiniones
[…]here are some hyperlinks to internet sites that we link to due to the fact we think they’re worth visiting[…]
عرب نار
[…]although web sites we backlink to beneath are considerably not associated to ours, we really feel they may be truly worth a go by way of, so possess a look[…]
video game key
[…]Here are a number of the sites we advise for our visitors[…]
anal vibrating cock ring
[…]that is the finish of this article. Right here you will obtain some internet sites that we believe youll value, just click the hyperlinks over[…]
best thrusting vibrators
[…]please pay a visit to the web sites we comply with, which includes this one, because it represents our picks from the web[…]
download pc games for windows
[…]Here are several of the web pages we advocate for our visitors[…]
apps for pc download
[…]below you will locate the link to some web sites that we believe you’ll want to visit[…]
apps download for pc
[…]Here are some of the web pages we recommend for our visitors[…]
celebrity pussy
[…]here are some links to internet sites that we link to for the reason that we feel they may be worth visiting[…]
games for pc download
[…]that may be the end of this report. Right here youll uncover some sites that we consider youll enjoy, just click the links over[…]
download apps apk for windows pc
[…]Sites of interest we’ve a link to[…]
cpanel hosting
[…]below youll uncover the link to some web pages that we believe you must visit[…]
passive monthly income investing
[…]Here are a number of the sites we advocate for our visitors[…]
WANZ-898
[…]one of our guests just lately suggested the following website[…]
free porn xxx
[…]Here are several of the sites we advise for our visitors[…]
girl using vibrator
[…]very couple of websites that come about to become detailed beneath, from our point of view are undoubtedly well really worth checking out[…]
download youtube videos
[…]although internet sites we backlink to beneath are considerably not associated to ours, we feel they’re truly worth a go via, so possess a look[…]
apk for windows 10 download
[…]very handful of web sites that happen to be comprehensive below, from our point of view are undoubtedly very well worth checking out[…]
pc games for windows 8
[…]Sites of interest we’ve a link to[…]
thc vape oil
[…]the time to study or stop by the content or sites we’ve linked to beneath the[…]
pc app
[…]Here are several of the internet sites we recommend for our visitors[…]
cruises from Sydney
[…]always a big fan of linking to bloggers that I adore but do not get a whole lot of link really like from[…]
Leila Sandor
[…]we like to honor quite a few other world-wide-web web pages around the internet, even when they arent linked to us, by linking to them. Underneath are some webpages really worth checking out[…]
mspy erfahrung
[…]we prefer to honor many other world wide web web-sites around the web, even though they arent linked to us, by linking to them. Below are some webpages really worth checking out[…]
DOCP 175
[…]that will be the end of this article. Right here youll find some sites that we assume youll enjoy, just click the links over[…]
bullet vibe
[…]we came across a cool web site that you just could appreciate. Take a look when you want[…]
Buy valium online
[…]Here are a number of the web sites we recommend for our visitors[…]
rechargeable bullet massager
[…]Sites of interest we have a link to[…]
Buy Fake Money
[…]we like to honor quite a few other world wide web web-sites around the net, even though they arent linked to us, by linking to them. Beneath are some webpages really worth checking out[…]
order trenbolone online
[…]very couple of sites that take place to be comprehensive below, from our point of view are undoubtedly nicely really worth checking out[…]
dual stimulation vibrator
[…]The information talked about within the post are some of the very best available […]
pc app for windows 8
[…]Every when inside a when we pick out blogs that we read. Listed beneath would be the most up-to-date web-sites that we opt for […]
Buy marijuana online
[…]just beneath, are various totally not associated internet sites to ours, having said that, they’re surely worth going over[…]
fake money for sale
[…]one of our visitors not long ago recommended the following website[…]
Paid Teaching
[…]Sites of interest we have a link to[…]
download app apk for windows
[…]although internet websites we backlink to below are considerably not associated to ours, we feel they may be really really worth a go by way of, so possess a look[…]
anal sex toy
[…]usually posts some incredibly interesting stuff like this. If you are new to this site[…]
free apk for laptop
[…]very couple of internet sites that happen to become comprehensive below, from our point of view are undoubtedly properly really worth checking out[…]
1950gSR
[…]Here is an excellent Blog You might Uncover Intriguing that we Encourage You[…]
magic wand review
[…]always a big fan of linking to bloggers that I appreciate but do not get a lot of link like from[…]
remote controlled vibrator
[…]although sites we backlink to below are considerably not associated to ours, we really feel they are actually worth a go by means of, so possess a look[…]
free download for pc windows
[…]although internet websites we backlink to beneath are considerably not related to ours, we feel they’re actually really worth a go via, so possess a look[…]
free download for pc
[…]although web-sites we backlink to below are considerably not related to ours, we really feel they are basically worth a go by, so have a look[…]
apk for windows 8 download
[…]Here are some of the web pages we advocate for our visitors[…]
buy xanax
[…]Here are a number of the web sites we advocate for our visitors[…]
porn
[…]always a huge fan of linking to bloggers that I love but dont get a great deal of link adore from[…]
cialis
[…]here are some hyperlinks to web pages that we link to mainly because we think they are worth visiting[…]
alcoholicsvictorious.org
[…]please go to the internet sites we stick to, like this one particular, because it represents our picks from the web[…]
stopoverdoseil.org
[…]Wonderful story, reckoned we could combine a couple of unrelated information, nonetheless genuinely worth taking a look, whoa did one particular find out about Mid East has got additional problerms at the same time […]
how to use a vibrator
[…]here are some hyperlinks to internet sites that we link to for the reason that we think they may be worth visiting[…]
FINCAR (1×10)
[…]that is the finish of this write-up. Right here you will find some sites that we believe you will value, just click the hyperlinks over[…]
best smm panel
[…]below youll find the link to some internet sites that we assume it is best to visit[…]
drywallers Burlington
[…]The info mentioned in the report are a few of the most effective out there […]
magic wand massager
[…]we came across a cool internet site that you just might get pleasure from. Take a look when you want[…]
sex swing door
[…]Here is a great Blog You might Come across Fascinating that we Encourage You[…]
bondage and restraints
[…]usually posts some extremely intriguing stuff like this. If youre new to this site[…]
bondage equipment
[…]the time to study or go to the content material or internet sites we’ve linked to beneath the[…]
kegel balls
[…]we like to honor lots of other online websites on the web, even though they arent linked to us, by linking to them. Underneath are some webpages really worth checking out[…]
anal strap on dildo
[…]check beneath, are some totally unrelated internet websites to ours, on the other hand, they may be most trustworthy sources that we use[…]
bathing bunny waterproof vibrator
[…]one of our visitors lately proposed the following website[…]
best realistic vibrating dildo
[…]Every once inside a although we choose blogs that we study. Listed beneath are the most current websites that we decide on […]
willy molding kit
[…]Sites of interest we’ve a link to[…]
viagra
[…]although web sites we backlink to below are considerably not connected to ours, we really feel they’re in fact worth a go by means of, so possess a look[…]
viagra
[…]The information and facts talked about within the article are a number of the best obtainable […]
porn toys
[…]that is the end of this article. Right here youll uncover some web sites that we consider you will appreciate, just click the hyperlinks over[…]
free download for windows pc
[…]the time to read or check out the material or websites we have linked to below the[…]
apps for pc download
[…]we like to honor quite a few other internet internet sites around the net, even if they arent linked to us, by linking to them. Underneath are some webpages really worth checking out[…]
free download for windows 7
[…]The details talked about within the report are a few of the top available […]
New Movies Releasing This Week
[…]The information talked about inside the article are a number of the top out there […]
legislation
[…]Wonderful story, reckoned we could combine a number of unrelated data, nonetheless genuinely really worth taking a appear, whoa did one learn about Mid East has got additional problerms also […]
dạy trang điểm chuyên nghiệp
[…]usually posts some extremely fascinating stuff like this. If youre new to this site[…]
xxx
[…]Wonderful story, reckoned we could combine a couple of unrelated information, nevertheless definitely worth taking a look, whoa did 1 study about Mid East has got much more problerms too […]
anal butt plug vibrator
[…]please visit the web sites we comply with, which includes this one particular, as it represents our picks in the web[…]
123P{!!HD!!}*
[…]below youll obtain the link to some websites that we assume it is best to visit[…]
Watch HD movie online for free.
[…]Here are a number of the web-sites we suggest for our visitors[…]
large dildo
[…]always a big fan of linking to bloggers that I appreciate but dont get a whole lot of link enjoy from[…]
FEELS GOOD
[…]Sites of interest we have a link to[…]
pornhub
[…]below you will find the link to some sites that we consider it is best to visit[…]
royal cbd
[…]The data mentioned in the write-up are a few of the most effective out there […]
viagra for men
[…]Every as soon as inside a while we pick out blogs that we read. Listed beneath are the most current sites that we choose […]
Kaspersky at the best price
[…]Every after inside a though we opt for blogs that we read. Listed below are the most current web sites that we pick out […]
best dildos
[…]check below, are some absolutely unrelated web sites to ours, however, they are most trustworthy sources that we use[…]
먹튀 검증
[…]Here are some of the web pages we advise for our visitors[…]
먹튀업체
[…]Sites of interest we’ve a link to[…]
dominos coupons
[…]please check out the web pages we adhere to, including this one particular, because it represents our picks from the web[…]
pizza hut coupon codes
[…]always a big fan of linking to bloggers that I like but really don’t get a great deal of link like from[…]
vibrating dong
[…]just beneath, are various entirely not associated internet sites to ours, on the other hand, they are certainly really worth going over[…]
bitcoin fpga algorithm
[…]Wonderful story, reckoned we could combine a couple of unrelated data, nonetheless definitely really worth taking a look, whoa did one master about Mid East has got a lot more problerms as well […]
nude
[…]just beneath, are numerous entirely not connected websites to ours, nonetheless, they’re certainly worth going over[…]
Quality Vacate Cleaning
[…]usually posts some extremely intriguing stuff like this. If youre new to this site[…]
apps download for windows 7
[…]below youll discover the link to some internet sites that we feel you ought to visit[…]
검증사이트
[…]below youll obtain the link to some websites that we believe you ought to visit[…]
adam and eve lube
[…]we came across a cool web-site that you could possibly appreciate. Take a look when you want[…]
안전한 우리카지노계열
[…]one of our visitors a short while ago encouraged the following website[…]
바다이야기
[…]that could be the finish of this write-up. Right here you will find some sites that we feel you will appreciate, just click the links over[…]
Bond back cleaners
[…]The facts mentioned in the article are a number of the ideal readily available […]
kinky
[…]here are some hyperlinks to sites that we link to since we believe they’re worth visiting[…]
메이저토토
[…]we came across a cool site that you could possibly appreciate. Take a search should you want[…]
먹튀사이트
[…]we like to honor a lot of other world wide web web-sites on the net, even if they arent linked to us, by linking to them. Under are some webpages worth checking out[…]
biiig stiiizy
[…]Here are some of the internet sites we advocate for our visitors[…]
chicken wings recipes
[…]very handful of web-sites that happen to be detailed below, from our point of view are undoubtedly nicely really worth checking out[…]
TylöHelo
[…]Every after in a whilst we opt for blogs that we study. Listed below would be the latest web-sites that we select […]
Secure Messenger
[…]check beneath, are some totally unrelated web-sites to ours, having said that, they’re most trustworthy sources that we use[…]
MVSD-410
[…]Here is a great Weblog You might Uncover Interesting that we Encourage You[…]
https://www.youtube.com/channel/UCdcAvAVLHQ6HLnHkHlGIeHg
[…]usually posts some extremely fascinating stuff like this. If you are new to this site[…]
body massager wand
[…]Wonderful story, reckoned we could combine a number of unrelated data, nonetheless definitely worth taking a search, whoa did 1 find out about Mid East has got more problerms at the same time […]
anal vibrator
[…]always a significant fan of linking to bloggers that I enjoy but dont get lots of link like from[…]
chomnes
[…]The info mentioned inside the article are a few of the most beneficial accessible […]
Whitney Simmons workout plan
[…]Sites of interest we’ve a link to[…]
free apps download for windows 10
[…]please visit the web pages we follow, such as this a single, because it represents our picks through the web[…]
app download for windows
[…]Here are a few of the web pages we suggest for our visitors[…]
free download for windows 10
[…]that could be the finish of this write-up. Right here you will uncover some web-sites that we consider you will appreciate, just click the links over[…]
free download for windows 10
[…]please check out the sites we adhere to, such as this one particular, because it represents our picks through the web[…]
pc app free download
[…]check beneath, are some entirely unrelated sites to ours, having said that, they may be most trustworthy sources that we use[…]
Plastic bags for the FMC market
[…]although web sites we backlink to beneath are considerably not associated to ours, we really feel they’re basically really worth a go as a result of, so possess a look[…]
software information submitter
[…]please pay a visit to the web pages we stick to, which includes this one, as it represents our picks in the web[…]
Book a escort
[…]here are some hyperlinks to websites that we link to for the reason that we assume they may be worth visiting[…]
broker business opportunity
[…]The facts mentioned within the article are several of the most beneficial available […]
HND 753
[…]we prefer to honor quite a few other world wide web web pages on the internet, even when they arent linked to us, by linking to them. Under are some webpages really worth checking out[…]
google adwords agency
[…]Here is a good Blog You might Locate Exciting that we Encourage You[…]
pocket pussy
[…]usually posts some extremely exciting stuff like this. If youre new to this site[…]
clit toys
[…]The facts mentioned in the article are a number of the most beneficial available […]
loadcentral free registration
[…]Here is a good Blog You may Come across Fascinating that we Encourage You[…]
steroids for sale
[…]Here is a good Weblog You may Come across Intriguing that we Encourage You[…]
an sang q10
[…]please go to the websites we comply with, which includes this one, because it represents our picks in the web[…]
http://www.seopublissoft.fr
[…]always a huge fan of linking to bloggers that I adore but really don’t get quite a bit of link love from[…]
hammer pulverizer
[…]Wonderful story, reckoned we could combine some unrelated data, nonetheless actually really worth taking a appear, whoa did one particular master about Mid East has got far more problerms as well […]
usyd canvas
[…]the time to study or visit the subject material or websites we have linked to below the[…]
food near me
[…]very handful of sites that happen to be detailed below, from our point of view are undoubtedly properly worth checking out[…]
mimblewimble scripting
[…]that may be the end of this write-up. Here you will find some sites that we assume you will value, just click the links over[…]
breakfast near me
[…]always a massive fan of linking to bloggers that I like but dont get quite a bit of link like from[…]
search engine optimisation agencies
[…]we came across a cool web page that you could possibly take pleasure in. Take a look for those who want[…]
free crm software online
[…]that would be the finish of this report. Right here youll uncover some web pages that we feel youll enjoy, just click the links over[…]
Make money with cryptocurrency
[…]Sites of interest we’ve a link to[…]
Contract Security Services
[…]one of our visitors recently suggested the following website[…]
Take my online class for me
[…]The data mentioned within the post are several of the most effective readily available […]
bitcoin doubler
[…]one of our guests a short while ago proposed the following website[…]
p spot orgasm
[…]just beneath, are numerous totally not related web pages to ours, even so, they’re certainly worth going over[…]
descargasmix
[…]usually posts some pretty fascinating stuff like this. If you are new to this site[…]
#Home
[…]we prefer to honor a lot of other net websites around the net, even if they arent linked to us, by linking to them. Under are some webpages really worth checking out[…]
dildos for women
[…]one of our guests recently proposed the following website[…]
sucking dildo
[…]here are some hyperlinks to websites that we link to since we assume they may be worth visiting[…]
dildo asmr
[…]that is the finish of this post. Right here youll uncover some internet sites that we think youll enjoy, just click the links over[…]
best dildo for double penetration
[…]the time to read or pay a visit to the subject material or web sites we have linked to beneath the[…]
hotels near me now
[…]check beneath, are some completely unrelated sites to ours, nevertheless, they’re most trustworthy sources that we use[…]
blackhat seo links
[…]Here are several of the websites we advocate for our visitors[…]
buy pbn links and facebook usa likes
[…]here are some hyperlinks to web pages that we link to mainly because we consider they’re worth visiting[…]
Anti-Oxidants
[…]one of our visitors not long ago recommended the following website[…]
vibrator
[…]Here are some of the web sites we suggest for our visitors[…]
s…
[…]below you will come across the link to some web-sites that we think you ought to visit[…]
123movies
[…]check beneath, are some absolutely unrelated websites to ours, on the other hand, they may be most trustworthy sources that we use[…]
lodges in springs
[…]Sites of interest we’ve a link to[…]
Buy fake google reviews
[…]please check out the web pages we follow, such as this one, because it represents our picks from the web[…]
토토웹사이트
[…]we came across a cool site that you just may delight in. Take a look for those who want[…]
rabbit toy
[…]Every once inside a whilst we choose blogs that we read. Listed beneath would be the most recent web sites that we pick out […]
퍼스트카지노
[…]check beneath, are some entirely unrelated internet sites to ours, even so, they’re most trustworthy sources that we use[…]
코인카지노
[…]we prefer to honor several other net websites around the web, even though they arent linked to us, by linking to them. Underneath are some webpages really worth checking out[…]
recipes
[…]Here is a superb Blog You may Come across Intriguing that we Encourage You[…]
SEX
[…]Here is an excellent Blog You might Uncover Interesting that we Encourage You[…]
web designing
[…]Every once in a though we pick out blogs that we study. Listed below would be the latest internet sites that we opt for […]
FREE SEX
[…]here are some links to web-sites that we link to since we think they’re really worth visiting[…]
Pizza near me
[…]we prefer to honor several other online sites on the web, even though they arent linked to us, by linking to them. Beneath are some webpages really worth checking out[…]
mens stroker
[…]we like to honor numerous other world-wide-web web-sites around the net, even when they arent linked to us, by linking to them. Underneath are some webpages worth checking out[…]
laweekly.com
[…]very handful of internet websites that take place to be detailed below, from our point of view are undoubtedly very well really worth checking out[…]
best bullet vibrator
[…]Here is an excellent Weblog You may Locate Interesting that we Encourage You[…]
indian baby photo shoot
[…]just beneath, are quite a few entirely not related websites to ours, even so, they may be certainly worth going over[…]
jelly dildo
[…]the time to read or check out the subject material or web sites we’ve linked to beneath the[…]
phen375 review
[…]Here is a great Blog You may Find Intriguing that we Encourage You[…]
flexible dildo
[…]Here is a good Blog You may Obtain Intriguing that we Encourage You[…]
Ford Ranger Raptor Bình Dương
[…]Sites of interest we have a link to[…]
male masturbator
[…]Wonderful story, reckoned we could combine a few unrelated data, nevertheless truly really worth taking a search, whoa did one learn about Mid East has got extra problerms too […]
Grey Cup Watch Here
[…]that may be the finish of this report. Here youll locate some sites that we consider you will appreciate, just click the links over[…]
South maui
[…]always a huge fan of linking to bloggers that I like but dont get a lot of link like from[…]
free apps download for windows 10,
[…]Every once in a while we pick blogs that we study. Listed beneath would be the most recent web-sites that we pick […]
apk for pc download,
[…]below youll come across the link to some web pages that we assume it is best to visit[…]
roblox
[…]Every after inside a whilst we select blogs that we read. Listed below would be the most current web pages that we opt for […]
best cbd oil for pain
[…]always a huge fan of linking to bloggers that I love but really don’t get a lot of link appreciate from[…]
dildo vibrator
[…]always a large fan of linking to bloggers that I adore but do not get a good deal of link love from[…]
rechargeable anal plug
[…]usually posts some really intriguing stuff like this. If youre new to this site[…]
best cbd oil for pain
[…]that will be the finish of this post. Here youll discover some web sites that we think youll enjoy, just click the hyperlinks over[…]
anal vibe
[…]one of our visitors a short while ago encouraged the following website[…]
vibrating penis extender
[…]Sites of interest we have a link to[…]
robux generator no human verification
[…]always a huge fan of linking to bloggers that I love but dont get quite a bit of link like from[…]
XXX VIDEOS
[…]just beneath, are numerous totally not associated websites to ours, nonetheless, they’re surely worth going over[…]
HotStamp Ribbon
[…]usually posts some extremely exciting stuff like this. If you are new to this site[…]
ETTORENT PORN DOWNLOAD
[…]usually posts some incredibly intriguing stuff like this. If youre new to this site[…]
cbd oil for depression
[…]check beneath, are some entirely unrelated websites to ours, however, they’re most trustworthy sources that we use[…]
cbd for insomnia
[…]one of our guests not too long ago proposed the following website[…]
pest control bradford
[…]below you will obtain the link to some web-sites that we think you ought to visit[…]
XXL DOWNLOAD
[…]one of our visitors not long ago advised the following website[…]
XNN VIDEO
[…]the time to study or go to the subject material or web sites we have linked to beneath the[…]
app for pc download
[…]always a massive fan of linking to bloggers that I like but dont get quite a bit of link like from[…]
free download for windows 10
[…]The info talked about inside the article are some of the top accessible […]
free download for windows 8
[…]just beneath, are numerous completely not associated websites to ours, even so, they may be surely worth going over[…]
PORNHUB
[…]very few websites that happen to become in depth below, from our point of view are undoubtedly very well worth checking out[…]
free download for windows 10
[…]just beneath, are various completely not related websites to ours, nevertheless, they may be surely worth going over[…]
chto takoe fomka
[…]we came across a cool web page that you may possibly take pleasure in. Take a look when you want[…]
sailboat charter croatia
[…]that may be the finish of this post. Right here you will find some web-sites that we feel youll appreciate, just click the hyperlinks over[…]
vibrator challenge
[…]that is the finish of this write-up. Right here you will obtain some websites that we feel you will appreciate, just click the hyperlinks over[…]
LEGO Friends Emmas Mobiele Dierenkliniek
[…]very couple of sites that happen to be detailed beneath, from our point of view are undoubtedly well worth checking out[…]
adam’s silicone dildo
[…]The facts mentioned within the article are a number of the most effective out there […]
cock ring
[…]we came across a cool website that you just may well love. Take a look in case you want[…]
anal sex
[…]the time to study or visit the content material or websites we have linked to beneath the[…]
super head honcho
[…]one of our guests not long ago encouraged the following website[…]
kips academy css notes
[…]Wonderful story, reckoned we could combine a number of unrelated data, nevertheless definitely worth taking a look, whoa did one understand about Mid East has got much more problerms too […]
prostate sex toy
[…]The information talked about inside the post are several of the best obtainable […]
panty vibe
[…]although websites we backlink to beneath are considerably not associated to ours, we feel they’re actually really worth a go by way of, so have a look[…]
anal plug
[…]Wonderful story, reckoned we could combine some unrelated data, nonetheless truly worth taking a look, whoa did one particular understand about Mid East has got extra problerms too […]
hiking trails near me
[…]that is the end of this article. Here youll discover some web-sites that we assume you will value, just click the hyperlinks over[…]
click here
[…]we like to honor lots of other world-wide-web web sites around the internet, even if they arent linked to us, by linking to them. Underneath are some webpages really worth checking out[…]
legionella testing kits
[…]that would be the end of this article. Right here youll discover some internet sites that we assume youll enjoy, just click the hyperlinks over[…]
우리카지노
[…]very couple of internet websites that occur to be detailed beneath, from our point of view are undoubtedly effectively worth checking out[…]
더킹카지노
[…]here are some hyperlinks to sites that we link to simply because we consider they may be worth visiting[…]
예스카지노
[…]always a major fan of linking to bloggers that I adore but do not get a good deal of link love from[…]
더나인카지노
[…]we like to honor many other web web pages around the web, even if they arent linked to us, by linking to them. Below are some webpages really worth checking out[…]
vibrating bullet
[…]the time to study or visit the subject material or websites we’ve linked to below the[…]
VePorn.com
[…]check beneath, are some totally unrelated sites to ours, nonetheless, they are most trustworthy sources that we use[…]
MKMP 315
[…]the time to read or check out the material or internet sites we have linked to below the[…]
예스카지노
[…]Every as soon as in a whilst we decide on blogs that we read. Listed beneath would be the most recent internet sites that we choose […]
퍼스트카지노
[…]The data talked about inside the write-up are a few of the top obtainable […]
더나인카지노
[…]Sites of interest we’ve a link to[…]
더킹카지노
[…]always a large fan of linking to bloggers that I enjoy but really don’t get a great deal of link enjoy from[…]
코인카지노
[…]usually posts some very interesting stuff like this. If you are new to this site[…]
Why. Who
[…]Every once in a while we decide on blogs that we study. Listed below are the most recent web sites that we decide on […]
CCRMG
[…]Wonderful story, reckoned we could combine some unrelated information, nevertheless really really worth taking a search, whoa did 1 master about Mid East has got much more problerms at the same time […]
Rottweiler breeder
[…]very few web-sites that occur to become comprehensive beneath, from our point of view are undoubtedly nicely worth checking out[…]
https://maps.google.cz/url?q=https%3A%2F%2Fphongkhamhana.com%2F
[…]very couple of web sites that occur to be comprehensive below, from our point of view are undoubtedly effectively really worth checking out[…]
ITALY VS SPAIN
[…]the time to study or go to the content material or web sites we have linked to beneath the[…]
english to afrikaans translation download
[…]below youll come across the link to some internet sites that we consider you ought to visit[…]
Jumpstart car Los Angeles
[…]the time to study or stop by the content material or sites we’ve linked to beneath the[…]
online research repository
[…]one of our guests a short while ago encouraged the following website[…]
vibrators for women
[…]please pay a visit to the sites we stick to, such as this one, as it represents our picks through the web[…]
rabbit ear toy
[…]Sites of interest we’ve a link to[…]
vedo izzy
[…]below you will discover the link to some sites that we believe you must visit[…]
CHEAP VIAGRA
[…]Wonderful story, reckoned we could combine a couple of unrelated information, nonetheless really worth taking a search, whoa did one particular learn about Mid East has got more problerms at the same time […]
couples dual pleasure ring
[…]Sites of interest we have a link to[…]
numbing lube
[…]here are some links to sites that we link to due to the fact we assume they are really worth visiting[…]
sex lingerie
[…]Here are a few of the internet sites we suggest for our visitors[…]
newborn photography india
[…]always a significant fan of linking to bloggers that I like but dont get quite a bit of link like from[…]
amateur creampie
[…]Sites of interest we’ve a link to[…]
vector art conversion
[…]Here is a superb Weblog You may Locate Fascinating that we Encourage You[…]
https://www.isaacroyston.com/
[…]usually posts some pretty fascinating stuff like this. If youre new to this site[…]
rc hobby store
[…]just beneath, are numerous absolutely not connected websites to ours, on the other hand, they are surely really worth going over[…]
liquid ketamine for sale
[…]usually posts some extremely intriguing stuff like this. If youre new to this site[…]
Hydrocodone for sale
[…]the time to study or check out the material or internet sites we’ve linked to below the[…]
Punch Newspaper
[…]although web-sites we backlink to beneath are considerably not connected to ours, we really feel they’re really really worth a go by means of, so have a look[…]
Rivers State Tourism
[…]very few web-sites that occur to become comprehensive beneath, from our point of view are undoubtedly very well really worth checking out[…]
Sims drive
[…]that would be the finish of this post. Here youll come across some web sites that we think youll appreciate, just click the links over[…]
Order Adderall online overnight
[…]below you will obtain the link to some sites that we feel you should visit[…]
best sucking vibrator
[…]although websites we backlink to beneath are considerably not related to ours, we feel they may be essentially worth a go through, so have a look[…]
san diego personal trainer
[…]although web sites we backlink to below are considerably not related to ours, we really feel they may be truly really worth a go via, so possess a look[…]
magic shop
[…]the time to study or visit the subject material or sites we’ve linked to below the[…]
mygiftcardsite
[…]although web sites we backlink to below are considerably not related to ours, we feel they may be in fact worth a go by, so possess a look[…]
takeout near me
[…]Wonderful story, reckoned we could combine a few unrelated information, nevertheless genuinely really worth taking a look, whoa did one discover about Mid East has got more problerms too […]
prepaidcardstatus.com
[…]please go to the internet sites we comply with, such as this 1, because it represents our picks from the web[…]
cbd oil near me
[…]check below, are some totally unrelated websites to ours, nevertheless, they’re most trustworthy sources that we use[…]
antec df 35
[…]The details mentioned in the report are a number of the most beneficial readily available […]
Wikipedia
[…]always a big fan of linking to bloggers that I appreciate but do not get quite a bit of link like from[…]
best vibrators
[…]below you will uncover the link to some internet sites that we assume you need to visit[…]
suits hoodie Jump suit plus size dressestailor near mebespoke
[…]we came across a cool site that you simply may well take pleasure in. Take a search in case you want[…]
navy blue shirt
[…]we prefer to honor numerous other world wide web web sites on the internet, even when they arent linked to us, by linking to them. Underneath are some webpages worth checking out[…]
trend i am boutique
[…]here are some hyperlinks to internet sites that we link to mainly because we assume they may be really worth visiting[…]
increase DR
[…]Wonderful story, reckoned we could combine a couple of unrelated information, nonetheless actually worth taking a search, whoa did one particular discover about Mid East has got a lot more problerms at the same time […]
https://blockchainafrica.site/
[…]Wonderful story, reckoned we could combine a number of unrelated data, nonetheless truly worth taking a look, whoa did 1 find out about Mid East has got more problerms as well […]
msn mail login
[…]Every as soon as inside a whilst we opt for blogs that we read. Listed beneath are the most current web-sites that we decide on […]
xnxc
[…]Here are some of the sites we advise for our visitors[…]
1040
[…]The info talked about in the article are a number of the best accessible […]
waterproof pocket massager
[…]the time to study or take a look at the content or web sites we’ve linked to beneath the[…]
male p spot massager
[…]check below, are some completely unrelated web-sites to ours, nevertheless, they may be most trustworthy sources that we use[…]
best cbd oil for pain
[…]although internet websites we backlink to beneath are considerably not associated to ours, we really feel they are essentially really worth a go via, so have a look[…]
mad science camp
[…]we came across a cool web-site that you simply could delight in. Take a appear in case you want[…]
best cbd gummies
[…]usually posts some extremely interesting stuff like this. If you are new to this site[…]
Naija School
[…]Every once inside a even though we pick blogs that we read. Listed below are the newest web pages that we pick […]
MP3 Songs
[…]check below, are some totally unrelated websites to ours, on the other hand, they may be most trustworthy sources that we use[…]
huge dildos
[…]that is the finish of this report. Right here youll uncover some internet sites that we assume you will value, just click the links over[…]
full apps download
[…]usually posts some pretty interesting stuff like this. If youre new to this site[…]
pc apps for windows 7
[…]that could be the finish of this write-up. Here youll locate some sites that we believe youll enjoy, just click the hyperlinks over[…]
free download for windows 7
[…]Here is a superb Weblog You may Obtain Intriguing that we Encourage You[…]
games for pc download
[…]Every once in a whilst we choose blogs that we study. Listed beneath are the newest web pages that we choose […]
games for pc download
[…]below youll find the link to some internet sites that we believe you must visit[…]
free app for pc downloadapp apk download for pc
[…]we came across a cool web site that you just may love. Take a appear should you want[…]
click here
[…]Every as soon as inside a even though we select blogs that we study. Listed beneath are the most current websites that we pick […]
free apps download for windows 8
[…]here are some hyperlinks to web-sites that we link to since we assume they may be worth visiting[…]
strap on dildo
[…]although internet websites we backlink to beneath are considerably not related to ours, we feel they are really worth a go through, so have a look[…]
rabbit vibrator
[…]here are some links to internet sites that we link to since we consider they’re really worth visiting[…]
stl aquarium sloth
[…]that will be the end of this write-up. Right here youll uncover some internet sites that we consider youll appreciate, just click the hyperlinks over[…]
best cbd oil for pain
[…]although internet sites we backlink to beneath are considerably not associated to ours, we really feel they may be basically really worth a go via, so have a look[…]
best cbd gummies
[…]although internet sites we backlink to below are considerably not connected to ours, we really feel they’re truly worth a go by means of, so have a look[…]
https://cleaningserviceofdc.com
[…]usually posts some quite fascinating stuff like this. If you are new to this site[…]
stroker sleeve
[…]very few websites that transpire to become in depth beneath, from our point of view are undoubtedly properly worth checking out[…]
vibrating wand massagers
[…]please stop by the web-sites we comply with, like this one, because it represents our picks in the web[…]
suction dildo
[…]we came across a cool website that you could delight in. Take a look should you want[…]
web design widnes
[…]we prefer to honor many other net web sites around the web, even though they arent linked to us, by linking to them. Below are some webpages really worth checking out[…]
realistic vibrating dildo
[…]check below, are some absolutely unrelated internet sites to ours, nevertheless, they’re most trustworthy sources that we use[…]
murang’a university of technology portal
[…]the time to study or pay a visit to the content or web pages we’ve linked to beneath the[…]
Free Ads
[…]Here is an excellent Weblog You might Find Fascinating that we Encourage You[…]
نقل عفش
[…]Every as soon as in a whilst we decide on blogs that we study. Listed below are the most up-to-date web pages that we select […]
UK vape shop
[…]just beneath, are various totally not associated web sites to ours, however, they are surely really worth going over[…]
etf
[…]the time to read or visit the material or web-sites we’ve linked to below the[…]
male enhancement pump
[…]although websites we backlink to beneath are considerably not connected to ours, we really feel they’re really worth a go by, so have a look[…]
710 Kingpen Cartridges
[…]Every once inside a while we decide on blogs that we read. Listed beneath would be the latest web pages that we opt for […]
Fruity Pebbles Strain
[…]check beneath, are some entirely unrelated websites to ours, on the other hand, they’re most trustworthy sources that we use[…]
Hydrocodone for Sale
[…]check beneath, are some absolutely unrelated web sites to ours, nevertheless, they are most trustworthy sources that we use[…]
http://www.headquarterscomplaints.com
[…]Wonderful story, reckoned we could combine several unrelated data, nevertheless seriously worth taking a appear, whoa did one particular understand about Mid East has got extra problerms too […]
satta king master
[…]the time to read or check out the content material or internet sites we have linked to below the[…]
pakistani daramas
[…]here are some hyperlinks to web pages that we link to because we consider they are really worth visiting[…]
edenrobe sale
[…]check beneath, are some completely unrelated web sites to ours, nonetheless, they’re most trustworthy sources that we use[…]
best toys for couples
[…]Every once in a though we opt for blogs that we study. Listed below would be the most up-to-date sites that we opt for […]
viagra
[…]just beneath, are a lot of completely not related web-sites to ours, even so, they may be certainly worth going over[…]
viagra
[…]below you will find the link to some web-sites that we believe you must visit[…]
viagra
[…]Wonderful story, reckoned we could combine some unrelated information, nevertheless actually worth taking a appear, whoa did 1 study about Mid East has got more problerms at the same time […]
Situs Poker Uang Asli
[…]the time to study or check out the content or internet sites we have linked to below the[…]
viagra
[…]please stop by the websites we adhere to, like this one particular, because it represents our picks from the web[…]
marijuana
[…]we came across a cool web site which you could possibly appreciate. Take a look in the event you want[…]
cannabis research
[…]Here are some of the web sites we advocate for our visitors[…]
Buy weed online
[…]below youll find the link to some websites that we believe you should visit[…]
Weed Wax
[…]just beneath, are many entirely not related web pages to ours, having said that, they’re certainly really worth going over[…]
Brass Knuckles Vape
[…]just beneath, are quite a few completely not related internet sites to ours, even so, they’re surely worth going over[…]
rechargeable rabbit vibrator
[…]Here is a superb Blog You may Discover Interesting that we Encourage You[…]
THC Vape Juice
[…]the time to study or pay a visit to the material or web pages we’ve linked to beneath the[…]
How Much is Joel Osteen Ticket
[…]check below, are some entirely unrelated websites to ours, on the other hand, they are most trustworthy sources that we use[…]
google maps seo services
[…]here are some hyperlinks to web sites that we link to due to the fact we assume they’re worth visiting[…]
agence digitale paris
[…]please go to the websites we follow, such as this one particular, because it represents our picks in the web[…]
cannabidiol
[…]always a massive fan of linking to bloggers that I adore but dont get a lot of link appreciate from[…]
buy cannabidiol oil
[…]Sites of interest we’ve a link to[…]
buy cbd oil
[…]Sites of interest we have a link to[…]
hacklink is your job
[…]very handful of internet sites that come about to be in depth below, from our point of view are undoubtedly well really worth checking out[…]
fda registration
[…]Sites of interest we have a link to[…]
Notarias en cancun
[…]Here is a superb Blog You might Find Intriguing that we Encourage You[…]
hacksaw blade distributors
[…]Here are a few of the internet sites we advocate for our visitors[…]
wand massager
[…]just beneath, are a lot of completely not related sites to ours, nevertheless, they are surely worth going over[…]
Gelato Strain
[…]the time to study or visit the content material or sites we have linked to below the[…]
marble
[…]the time to read or stop by the subject material or internet sites we’ve linked to below the[…]
Vape shops
[…]we like to honor numerous other web web sites around the web, even though they arent linked to us, by linking to them. Underneath are some webpages really worth checking out[…]
malibu lyrics
[…]please check out the web pages we adhere to, including this one particular, as it represents our picks in the web[…]
INDIAN VISA
[…]we prefer to honor several other world wide web internet sites around the internet, even when they arent linked to us, by linking to them. Below are some webpages really worth checking out[…]
mens toys gadgets
[…]one of our guests just lately recommended the following website[…]
Order aderall online
[…]please pay a visit to the web pages we stick to, like this one particular, because it represents our picks through the web[…]
gls training
[…]we came across a cool web-site which you could appreciate. Take a search if you want[…]
science quizzes
[…]always a big fan of linking to bloggers that I appreciate but do not get a great deal of link adore from[…]
cbd oil for dogs
[…]although internet websites we backlink to beneath are considerably not connected to ours, we feel they are in fact worth a go via, so possess a look[…]
vibrator
[…]usually posts some really intriguing stuff like this. If youre new to this site[…]
Perth Breakfast
[…]Wonderful story, reckoned we could combine a few unrelated data, nonetheless truly really worth taking a appear, whoa did 1 learn about Mid East has got more problerms also […]
Buy tramadol online legally
[…]Wonderful story, reckoned we could combine a number of unrelated information, nonetheless definitely really worth taking a search, whoa did one particular understand about Mid East has got far more problerms too […]
Malaysia Online Casino
[…]we like to honor many other online websites around the net, even when they arent linked to us, by linking to them. Under are some webpages really worth checking out[…]
Buy oxycodone online legally
[…]below youll find the link to some internet sites that we think you’ll want to visit[…]
Buy Mdma chrystal Online
[…]The data talked about inside the article are a number of the most effective accessible […]
order id card online nc
[…]please pay a visit to the web sites we comply with, which includes this a single, because it represents our picks from the web[…]
Cannabis Oil
[…]the time to study or visit the subject material or sites we have linked to below the[…]
pornographie
[…]Here are a number of the internet sites we suggest for our visitors[…]
Cyber Security Expert in India
[…]we like to honor lots of other net web sites around the net, even if they arent linked to us, by linking to them. Under are some webpages really worth checking out[…]
inexpensive seo services
[…]always a big fan of linking to bloggers that I like but dont get quite a bit of link really like from[…]
Buy Marijuana Online
[…]that is the end of this write-up. Right here you will discover some sites that we feel youll value, just click the links over[…]
industrial hemp
[…]very couple of internet sites that come about to become detailed beneath, from our point of view are undoubtedly very well really worth checking out[…]
vibrating anal beads
[…]Here is a good Blog You may Obtain Interesting that we Encourage You[…]
suction cup dildos
[…]The info talked about in the write-up are several of the top readily available […]
hasta yatağı kiralama
[…]we like to honor a lot of other net websites around the net, even if they arent linked to us, by linking to them. Underneath are some webpages really worth checking out[…]
http://boise.bizlistusa.com/business/5213557.htm
[…]Every when inside a though we decide on blogs that we study. Listed below are the newest websites that we opt for […]
MrPornGeek
[…]always a major fan of linking to bloggers that I really like but dont get lots of link appreciate from[…]
Leathercraft
[…]just beneath, are several totally not connected web-sites to ours, however, they’re surely worth going over[…]
http://www.qtellbuyandsell.com/456/posts/8-Business-to-Business-/232–Business-Opportunities/180403-Mold-Removal-Boise.html
[…]check below, are some completely unrelated sites to ours, on the other hand, they may be most trustworthy sources that we use[…]
electrical panel upgrade
[…]below you will locate the link to some internet sites that we feel it is best to visit[…]
cbd oil near me
[…]that will be the finish of this article. Right here you will locate some web sites that we consider youll appreciate, just click the links over[…]
fapidy.com
[…]we like to honor a lot of other world wide web web sites around the net, even though they arent linked to us, by linking to them. Under are some webpages worth checking out[…]
VoIP Services
[…]although web-sites we backlink to beneath are considerably not connected to ours, we feel they’re in fact really worth a go through, so have a look[…]
Buy Weed Online
[…]Sites of interest we have a link to[…]
тест на дюзи
[…]we came across a cool web-site that you just may well enjoy. Take a search for those who want[…]
private chef
[…]we prefer to honor lots of other web web sites around the net, even when they arent linked to us, by linking to them. Underneath are some webpages really worth checking out[…]
Amazon fire TV stick 4K
Tech Addiction Media is a blogging platform providing tutorials, ideas and information on entertainment using streaming technology for home and business, and also provides information relating to social media, marketing, entrepreneurship, and technolog…
Royal CBD oil
[…]just beneath, are several completely not associated web pages to ours, however, they’re surely really worth going over[…]
https://www.dailyrealestatestudy.com/your-heater-the-forgotten-utility-vehicle-of-your-home-in-illinois/
[…]usually posts some pretty interesting stuff like this. If youre new to this site[…]
CBD gummies for stress
[…]Here are some of the websites we recommend for our visitors[…]
how it’s made dildo
[…]that will be the finish of this article. Right here you will discover some websites that we believe youll appreciate, just click the hyperlinks over[…]
naasongs
[…]very couple of web sites that occur to become comprehensive beneath, from our point of view are undoubtedly nicely really worth checking out[…]
https://www.southjordanjournal.com/businesses/nc-fayetteville-fayetteville-roofing-services
[…]we like to honor several other internet web-sites on the net, even when they arent linked to us, by linking to them. Beneath are some webpages really worth checking out[…]
bluetooth panties
[…]Here is a superb Weblog You might Find Fascinating that we Encourage You[…]
apps for pc download
[…]one of our guests just lately suggested the following website[…]
free download for windows 10
[…]we came across a cool web site that you just might delight in. Take a look in the event you want[…]
full version pc games download
[…]just beneath, are a lot of entirely not connected sites to ours, on the other hand, they’re surely worth going over[…]
http://landscapereuix25814.bluxeblog.com/20061264/indicators-on-carpet-cleaning-cost-you-should-know
[…]Sites of interest we’ve a link to[…]
https://superfastmoney.org/
[…]below youll discover the link to some web sites that we believe you need to visit[…]
Dank cartrifges
[…]check below, are some absolutely unrelated internet sites to ours, on the other hand, they’re most trustworthy sources that we use[…]
G spot rabbit vibrator
[…]please check out the websites we comply with, such as this one particular, as it represents our picks from the web[…]
Vibrating strapon dildo
[…]here are some links to websites that we link to mainly because we feel they may be worth visiting[…]
http://www.genina.com/user/editDone/812648.page
[…]although web-sites we backlink to beneath are considerably not connected to ours, we really feel they’re basically really worth a go by way of, so possess a look[…]
submissive
[…]please stop by the internet sites we follow, like this a single, because it represents our picks from the web[…]
first time
[…]just beneath, are many totally not related web sites to ours, on the other hand, they may be certainly really worth going over[…]
Sex Toy Unboxing
[…]we like to honor numerous other online web sites on the web, even if they arent linked to us, by linking to them. Beneath are some webpages worth checking out[…]
best software review
[…]Every once in a though we select blogs that we read. Listed below are the latest web pages that we pick out […]
egged tours petra
[…]here are some hyperlinks to sites that we link to due to the fact we feel they may be worth visiting[…]
CBD products
[…]always a massive fan of linking to bloggers that I enjoy but really don’t get a whole lot of link like from[…]
https://diamondcleaningusa.com/carpet-cleaning/
[…]check below, are some totally unrelated internet sites to ours, nonetheless, they are most trustworthy sources that we use[…]
merle corgi puppies
[…]we came across a cool web-site which you could possibly get pleasure from. Take a appear if you want[…]
crm software for architectural firm
[…]Wonderful story, reckoned we could combine several unrelated data, nevertheless genuinely really worth taking a appear, whoa did 1 master about Mid East has got a lot more problerms at the same time […]
equipment financing
[…]we like to honor lots of other web internet sites on the internet, even if they arent linked to us, by linking to them. Underneath are some webpages worth checking out[…]
furniture shops in gurgaon
[…]Wonderful story, reckoned we could combine a handful of unrelated information, nevertheless truly really worth taking a appear, whoa did a single discover about Mid East has got additional problerms also […]
buy CBD products
[…]Every when in a whilst we choose blogs that we study. Listed beneath are the most up-to-date web sites that we pick […]
onhax spotify
[…]always a massive fan of linking to bloggers that I like but really don’t get a whole lot of link like from[…]
Online Advertising
[…]below youll locate the link to some web-sites that we feel you should visit[…]
THC Vape Oil
[…]Sites of interest we have a link to[…]
flight
[…]please check out the sites we comply with, including this one, because it represents our picks through the web[…]
https://myinforms.com/
[…]The info talked about inside the article are several of the best obtainable […]
chemical waterproofing
[…]Sites of interest we’ve a link to[…]
FemaleAgent Amazing Asian sensation
[…]here are some hyperlinks to sites that we link to mainly because we feel they are really worth visiting[…]
Cannabis Oil
[…]check below, are some entirely unrelated web sites to ours, however, they are most trustworthy sources that we use[…]
cbd full spectrum
[…]Here is a superb Blog You might Locate Exciting that we Encourage You[…]
https://federicocalderon.com/real-estate-las-vegas
[…]the time to study or stop by the subject material or sites we’ve linked to beneath the[…]
fda cbd
[…]usually posts some incredibly intriguing stuff like this. If you are new to this site[…]
ctfo cbd
[…]Wonderful story, reckoned we could combine a couple of unrelated data, nevertheless genuinely really worth taking a search, whoa did one particular understand about Mid East has got extra problerms too […]
royal cbd
[…]Here are several of the sites we advise for our visitors[…]
cbd gummies
[…]The information talked about within the article are a number of the very best readily available […]
domain authority
[…]below you will come across the link to some internet sites that we believe you should visit[…]
https://mksorb.com/ccleaner-pro-apk/
[…]Every when in a when we opt for blogs that we study. Listed beneath are the most recent web-sites that we select […]
Buy Backlinks
[…]usually posts some quite interesting stuff like this. If youre new to this site[…]
https://5starlegitdocuments.com/counterfeit-money/
[…]The details talked about in the article are some of the best obtainable […]
https://mksorb.com/security-master-antivirus-apk/
[…]below you will find the link to some web sites that we believe it is best to visit[…]
https://mksorb.com/malwarebytes-security-premium-apk/
[…]here are some hyperlinks to web-sites that we link to due to the fact we believe they’re worth visiting[…]
vibrating butt plug
[…]Wonderful story, reckoned we could combine a handful of unrelated data, nonetheless definitely really worth taking a look, whoa did one find out about Mid East has got additional problerms at the same time […]
wireless vibrating panties
[…]Here are a few of the internet sites we recommend for our visitors[…]
Loan App Contact
[…]just beneath, are quite a few completely not related websites to ours, on the other hand, they’re surely worth going over[…]
https://mksorb.com/aio-launcher-pro-apk/
[…]we like to honor a lot of other online web pages around the web, even though they arent linked to us, by linking to them. Underneath are some webpages worth checking out[…]
Wife
[…]very handful of web-sites that come about to be detailed beneath, from our point of view are undoubtedly very well really worth checking out[…]
Tips
[…]The information and facts mentioned within the post are some of the top accessible […]
dual motor vibrator
[…]although websites we backlink to below are considerably not related to ours, we really feel they are truly worth a go by way of, so possess a look[…]
https://mksorb.com/kinemaster-pro-apk/
[…]please stop by the sites we follow, which includes this a single, because it represents our picks through the web[…]
jack rabbit toy
[…]The data talked about in the report are a number of the top available […]
https://mksorb.com/thunder-vpn-pro-apk/
[…]The data mentioned inside the report are several of the most effective offered […]
remote control bullet vibrator
[…]Sites of interest we’ve a link to[…]
https://mksorb.com/assassins-creed-rebellion-mod-apk/
[…]usually posts some really exciting stuff like this. If youre new to this site[…]
Homeowners
[…]Wonderful story, reckoned we could combine a couple of unrelated information, nonetheless genuinely worth taking a appear, whoa did 1 discover about Mid East has got extra problerms at the same time […]
delhi to phuket packages
[…]Here is a superb Weblog You may Locate Exciting that we Encourage You[…]
русский язык в упражнениях
[…]usually posts some quite fascinating stuff like this. If youre new to this site[…]
Authentic Stiiizy
[…]please stop by the sites we adhere to, which includes this a single, because it represents our picks in the web[…]
instagram management services in india
[…]here are some links to web pages that we link to for the reason that we assume they’re really worth visiting[…]
раскраски для взрослых
[…]here are some hyperlinks to web-sites that we link to since we assume they are really worth visiting[…]
http://knsz.prz.edu.pl/forum/member.php?action=profile&uid=321623
[…]check below, are some entirely unrelated internet sites to ours, even so, they are most trustworthy sources that we use[…]
North Webster Indiana
[…]Every as soon as in a even though we opt for blogs that we study. Listed beneath are the newest web sites that we pick out […]
cannabis for the culture
[…]the time to study or check out the content or websites we’ve linked to beneath the[…]
cannabis
[…]Every after in a whilst we pick blogs that we read. Listed beneath would be the most current internet sites that we decide on […]
cannabis for the culture
[…]that will be the end of this write-up. Right here youll discover some web-sites that we consider you will enjoy, just click the links over[…]
cannabis for the culture
[…]Sites of interest we’ve a link to[…]
virtual prepaid visa card provider
[…]here are some hyperlinks to web-sites that we link to since we think they are really worth visiting[…]
https://mksorb.com/photo-editor-aviary-apk/
[…]Every once in a whilst we opt for blogs that we read. Listed beneath would be the most recent websites that we decide on […]
visa and MasterCard
[…]Here is a superb Weblog You might Locate Exciting that we Encourage You[…]
news
[…]that may be the end of this post. Here you will find some internet sites that we consider you will value, just click the hyperlinks over[…]
indian visa online
[…]the time to study or go to the content or web-sites we’ve linked to beneath the[…]
sexygirls shows
[…]below you will uncover the link to some web-sites that we assume you’ll want to visit[…]
sex streaming
[…]Every the moment in a whilst we choose blogs that we study. Listed beneath are the most current websites that we choose […]
MKsOrb
[…]check beneath, are some totally unrelated internet websites to ours, even so, they are most trustworthy sources that we use[…]
MKsOrb.Com
[…]Here is an excellent Weblog You may Discover Intriguing that we Encourage You[…]
MKsOrb.Com
[…]just beneath, are several totally not associated web-sites to ours, having said that, they are certainly worth going over[…]
MKsOrb.Com
[…]please go to the websites we stick to, including this 1, because it represents our picks from the web[…]
MKsOrb
[…]Wonderful story, reckoned we could combine some unrelated data, nonetheless seriously really worth taking a appear, whoa did a single learn about Mid East has got additional problerms also […]
CBD Isolate
[…]here are some links to websites that we link to since we think they are really worth visiting[…]
Office Cleaning Las Vegas
[…]the time to read or pay a visit to the subject material or web pages we’ve linked to below the[…]
MKsOrb
[…]we came across a cool website that you just may possibly delight in. Take a look should you want[…]
candles
[…]we like to honor numerous other internet sites around the net, even if they arent linked to us, by linking to them. Below are some webpages worth checking out[…]
sexy cams live
[…]check beneath, are some totally unrelated sites to ours, nonetheless, they may be most trustworthy sources that we use[…]
MKsOrb.Com
[…]below you will locate the link to some web sites that we consider you ought to visit[…]
sexy
[…]we prefer to honor many other web web sites around the internet, even when they arent linked to us, by linking to them. Underneath are some webpages really worth checking out[…]
MKsOrb
[…]very handful of web sites that happen to become in depth below, from our point of view are undoubtedly very well worth checking out[…]
MKsOrb.Com
[…]one of our visitors not long ago recommended the following website[…]
детские аудио книги
[…]just beneath, are numerous entirely not associated websites to ours, on the other hand, they are certainly really worth going over[…]
Best Link Shortener
[…]please check out the web pages we stick to, including this one, because it represents our picks from the web[…]
Android
[…]please take a look at the web pages we comply with, like this one, as it represents our picks in the web[…]
Dispensary Near Me
[…]one of our visitors lately proposed the following website[…]
Free Download
[…]Sites of interest we’ve a link to[…]
APK
[…]Every as soon as inside a although we pick out blogs that we study. Listed below would be the newest sites that we pick […]
https://royalcbd.com/product/cbd-oil-2500mg/
[…]very couple of web sites that come about to become detailed below, from our point of view are undoubtedly well worth checking out[…]
https://royalcbd.com/product/cbd-gummies-10mg/
[…]Every when in a although we pick blogs that we read. Listed beneath are the most current web-sites that we opt for […]
https://royalcbd.com/product/cbd-oil-500mg/
[…]below youll uncover the link to some sites that we believe you must visit[…]
apk
[…]please check out the web sites we stick to, including this one particular, because it represents our picks through the web[…]
https://royalcbd.com/product/cbd-capsules-25mg/
[…]usually posts some very intriguing stuff like this. If youre new to this site[…]
https://royalcbd.com/product/cbd-salve/
[…]one of our guests recently advised the following website[…]
http://googlestrends.com/
[…]Every after inside a even though we opt for blogs that we study. Listed beneath are the latest web-sites that we opt for […]
Coinpunk
[…]check below, are some completely unrelated sites to ours, nonetheless, they may be most trustworthy sources that we use[…]
coinchomp
[…]check beneath, are some entirely unrelated web-sites to ours, having said that, they’re most trustworthy sources that we use[…]
Yiffalicious
[…]always a large fan of linking to bloggers that I really like but really don’t get a whole lot of link appreciate from[…]
MKsOrb.Com
[…]Here is an excellent Blog You might Find Exciting that we Encourage You[…]
how to use a dildo
[…]that will be the end of this article. Here you will come across some web pages that we feel you will value, just click the hyperlinks over[…]
Business Apps
[…]check below, are some absolutely unrelated internet sites to ours, however, they are most trustworthy sources that we use[…]
MKsOrb.Com
[…]usually posts some very fascinating stuff like this. If you are new to this site[…]
کوس
[…]the time to study or take a look at the subject material or web-sites we have linked to beneath the[…]
THC vape juice
[…]we came across a cool web-site that you just could possibly love. Take a search in the event you want[…]
MKsOrb
[…]Wonderful story, reckoned we could combine a few unrelated data, nevertheless seriously really worth taking a search, whoa did 1 master about Mid East has got additional problerms at the same time […]
MKsOrb.Com
[…]Here is a superb Blog You might Come across Exciting that we Encourage You[…]
Pet store
[…]here are some hyperlinks to web-sites that we link to because we feel they may be really worth visiting[…]
MKsOrb
[…]the time to read or stop by the material or websites we have linked to beneath the[…]
buy reptiles online
[…]here are some hyperlinks to websites that we link to simply because we consider they may be worth visiting[…]
MKsOrb.Com
[…]Every after in a even though we choose blogs that we read. Listed beneath would be the newest internet sites that we opt for […]
MKsOrb.Com
[…]Here are some of the websites we recommend for our visitors[…]
Maltipoo puppy
[…]Sites of interest we have a link to[…]
Thc vape juice
[…]one of our visitors recently recommended the following website[…]
MKsOrb.Com
[…]although internet sites we backlink to beneath are considerably not related to ours, we feel they are essentially really worth a go by means of, so possess a look[…]
English bulldog puppies for sale
[…]one of our guests recently proposed the following website[…]
blue applehead chihuahua puppies for sale
[…]the time to study or go to the material or web sites we have linked to below the[…]
French bulldog for sale near me
[…]one of our guests just lately advised the following website[…]
Dank vapes
[…]Here is a good Blog You might Discover Interesting that we Encourage You[…]
http://buycounterfeitmoneyonline.net
[…]here are some hyperlinks to web pages that we link to for the reason that we assume they may be really worth visiting[…]
rottweiler puppies for sale near me
[…]here are some hyperlinks to sites that we link to simply because we believe they may be worth visiting[…]
border collie mix puppies for sale near me
[…]we like to honor numerous other net internet sites around the web, even though they arent linked to us, by linking to them. Underneath are some webpages really worth checking out[…]
german shepherd for sale
[…]The information talked about inside the post are several of the ideal accessible […]
buying ketamine
[…]one of our guests a short while ago proposed the following website[…]
Dank vapes
[…]always a big fan of linking to bloggers that I adore but really don’t get a good deal of link love from[…]
https://counterfeitmoneyforsale.online/
[…]Every after in a when we pick blogs that we read. Listed below would be the most recent web pages that we decide on […]
best penis pump
[…]here are some hyperlinks to sites that we link to simply because we consider they may be worth visiting[…]
penis enlargement pumps
[…]The information talked about inside the post are some of the most effective obtainable […]
CBD
[…]that may be the finish of this report. Right here youll find some web-sites that we assume youll appreciate, just click the hyperlinks over[…]
CBD
[…]below you will find the link to some internet sites that we consider you must visit[…]
oneplus 8
[…]just beneath, are quite a few totally not associated web sites to ours, nevertheless, they are certainly worth going over[…]
CBD
[…]Here is a superb Weblog You may Come across Intriguing that we Encourage You[…]
CBD
[…]the time to study or pay a visit to the material or web-sites we’ve linked to below the[…]
CBD
[…]we like to honor several other web websites around the web, even though they arent linked to us, by linking to them. Beneath are some webpages worth checking out[…]
CBD
[…]although websites we backlink to beneath are considerably not connected to ours, we feel they’re really worth a go by way of, so have a look[…]
CBD
[…]here are some hyperlinks to sites that we link to for the reason that we consider they may be worth visiting[…]
CBD
[…]below youll uncover the link to some web pages that we feel you need to visit[…]
buy CBD oil
[…]Here is a great Weblog You may Locate Interesting that we Encourage You[…]
buy CBD oil
[…]Here is a good Weblog You might Find Intriguing that we Encourage You[…]
CBD oil
[…]one of our guests recently encouraged the following website[…]
CBD oil
[…]usually posts some really interesting stuff like this. If you are new to this site[…]
https://freereviewnow.com/
[…]the time to read or go to the content material or sites we have linked to beneath the[…]
stretchy penis ring
[…]here are some links to web-sites that we link to for the reason that we feel they’re really worth visiting[…]
royal cbd products
[…]Here is an excellent Blog You might Come across Exciting that we Encourage You[…]
best cbd
[…]one of our visitors lately proposed the following website[…]
royal cbd products
[…]the time to read or visit the subject material or websites we’ve linked to beneath the[…]
JUULPODS NEAR ME
[…]The details talked about in the report are some of the most effective available […]
CBD gummies
[…]Every as soon as inside a although we choose blogs that we read. Listed beneath are the newest sites that we pick […]
CBD gummies
[…]Sites of interest we have a link to[…]
app free download for windows 10
[…]Here are several of the internet sites we suggest for our visitors[…]
free windows app download
[…]here are some hyperlinks to web pages that we link to due to the fact we believe they are really worth visiting[…]
free app download
[…]always a big fan of linking to bloggers that I appreciate but really don’t get a good deal of link enjoy from[…]
apps for pc
[…]Sites of interest we’ve a link to[…]
free laptop games download
[…]below youll find the link to some websites that we think you ought to visit[…]
app free download
[…]we came across a cool web page that you simply could possibly love. Take a appear when you want[…]
free download for windows
[…]although sites we backlink to beneath are considerably not connected to ours, we really feel they’re essentially really worth a go via, so have a look[…]
app free download
[…]usually posts some pretty exciting stuff like this. If you are new to this site[…]
free app for pclaptop
[…]below youll come across the link to some internet sites that we consider you’ll want to visit[…]
games for pc download
[…]Here are several of the sites we recommend for our visitors[…]
free pc games download
[…]check beneath, are some completely unrelated web-sites to ours, even so, they’re most trustworthy sources that we use[…]
free download for windows
[…]we came across a cool web-site that you may delight in. Take a search for those who want[…]
FabHotels Coupons
[…]Sites of interest we have a link to[…]
react native
[…]the time to study or go to the content or web-sites we’ve linked to beneath the[…]
nill
[…]usually posts some really intriguing stuff like this. If you are new to this site[…]
foreplay sex
[…]although internet sites we backlink to below are considerably not connected to ours, we really feel they’re essentially really worth a go via, so have a look[…]
best male mastubator
[…]Sites of interest we have a link to[…]
Deep Spin Poster
[…]that will be the end of this report. Here you will come across some websites that we think you will enjoy, just click the hyperlinks over[…]
Ministeck prijs
[…]usually posts some incredibly fascinating stuff like this. If youre new to this site[…]
8 inch dildo
[…]Wonderful story, reckoned we could combine some unrelated information, nevertheless definitely worth taking a search, whoa did one discover about Mid East has got a lot more problerms also […]
Cannabis Oil
[…]Here is a good Blog You might Obtain Intriguing that we Encourage You[…]
Vape Shop Near Me
[…]Here is a great Weblog You might Locate Exciting that we Encourage You[…]
CBD capsules
[…]we prefer to honor numerous other world wide web web-sites around the web, even though they arent linked to us, by linking to them. Underneath are some webpages worth checking out[…]
CBD soft gels
[…]here are some hyperlinks to websites that we link to for the reason that we think they’re worth visiting[…]
yusufçuk kolye
[…]one of our visitors recently advised the following website[…]
Most Profitable Customer
[…]although internet sites we backlink to beneath are considerably not associated to ours, we really feel they may be basically worth a go by, so have a look[…]
CBD oils
[…]we came across a cool web-site that you simply might enjoy. Take a appear for those who want[…]
male stroker toy
[…]Every when inside a even though we choose blogs that we study. Listed beneath are the most recent web-sites that we decide on […]
hairdressing scissors
[…]that is the end of this article. Right here you will discover some web sites that we feel youll appreciate, just click the links over[…]
CBS oil benefits
[…]Every the moment inside a although we pick blogs that we read. Listed beneath are the newest websites that we select […]
professional hairdressing scissors
[…]please go to the internet sites we adhere to, including this a single, because it represents our picks through the web[…]
barbering scissors
[…]Wonderful story, reckoned we could combine a few unrelated information, nevertheless really really worth taking a appear, whoa did one particular master about Mid East has got extra problerms also […]
Mark Konrad Chinese Scissors
[…]the time to study or go to the content material or web sites we’ve linked to below the[…]
solution clé en main automatisées
[…]the time to read or pay a visit to the subject material or web pages we have linked to below the[…]
hairdressing scissors icandy
[…]always a huge fan of linking to bloggers that I like but do not get quite a bit of link really like from[…]
hairdressing scissors
[…]very handful of internet sites that take place to be comprehensive beneath, from our point of view are undoubtedly nicely worth checking out[…]
cbd oil Australia
[…]Every after inside a while we pick blogs that we read. Listed beneath would be the most up-to-date web sites that we opt for […]
VAPE CARTRIDGES
[…]although internet sites we backlink to below are considerably not connected to ours, we really feel they may be essentially really worth a go by, so possess a look[…]
solar panel kit
[…]check below, are some totally unrelated web-sites to ours, even so, they are most trustworthy sources that we use[…]
mens rings online
[…]always a large fan of linking to bloggers that I love but dont get a whole lot of link adore from[…]
free download for pc windows
[…]one of our guests not long ago recommended the following website[…]
free download for windows 10
[…]we came across a cool web-site that you may well take pleasure in. Take a search for those who want[…]
app free download for windows 8
[…]just beneath, are various entirely not related sites to ours, however, they are surely worth going over[…]
apps download for pc
[…]Sites of interest we’ve a link to[…]
free download for windows pc
[…]just beneath, are a lot of entirely not connected sites to ours, on the other hand, they’re certainly really worth going over[…]
games download for pc
[…]just beneath, are several completely not associated web pages to ours, nevertheless, they’re surely worth going over[…]
app free download for windows 8
[…]the time to study or go to the subject material or websites we’ve linked to below the[…]
virtual visa card buy
[…]very couple of sites that come about to be in depth below, from our point of view are undoubtedly effectively really worth checking out[…]
cannabis oil for sale
[…]The details talked about in the article are several of the top available […]
kharkov university
[…]usually posts some extremely intriguing stuff like this. If youre new to this site[…]
hairdressing scissors matsui
[…]always a significant fan of linking to bloggers that I appreciate but do not get a great deal of link like from[…]
cash for scrap cars calgary
[…]usually posts some really exciting stuff like this. If youre new to this site[…]
elite chinese scissors
[…]just beneath, are a lot of totally not associated web pages to ours, even so, they are surely worth going over[…]
best CBD oil
[…]very few web sites that occur to be in depth beneath, from our point of view are undoubtedly effectively worth checking out[…]
best CBD gummies
[…]below youll obtain the link to some web sites that we feel you must visit[…]
Chiang Mai
[…]that would be the finish of this write-up. Right here you will locate some web pages that we assume youll value, just click the hyperlinks over[…]
scraping api
[…]below you will uncover the link to some web-sites that we assume you must visit[…]
CBD gummies
[…]one of our visitors not too long ago advised the following website[…]
CBD products
[…]just beneath, are several entirely not associated websites to ours, on the other hand, they may be surely worth going over[…]
wholesale paddle boards
[…]here are some hyperlinks to web sites that we link to because we believe they are worth visiting[…]
free download for windows 7
[…]one of our guests not too long ago encouraged the following website[…]
vibrators for women
[…]we came across a cool web page that you just could appreciate. Take a appear if you want[…]
cheap male mastubator
[…]Here are some of the sites we advocate for our visitors[…]
realistic vibrators
[…]one of our guests recently suggested the following website[…]
best CBD capsules
[…]one of our guests recently recommended the following website[…]
strap on toys
[…]the time to read or go to the content or websites we’ve linked to below the[…]
suction dildo
[…]Wonderful story, reckoned we could combine some unrelated data, nonetheless truly worth taking a appear, whoa did a single master about Mid East has got more problerms as well […]
porno
[…]Here is a superb Weblog You may Locate Fascinating that we Encourage You[…]
anal play
[…]we came across a cool internet site that you simply could take pleasure in. Take a appear in the event you want[…]
generic ventolin
Listening Room Acoustics: Room Modes and Standing Waves – NOVO Audio and Technology Magazine
cock extension
[…]we prefer to honor many other online sites around the web, even when they arent linked to us, by linking to them. Beneath are some webpages worth checking out[…]
best cbd cream for pain
[…]check below, are some completely unrelated websites to ours, however, they are most trustworthy sources that we use[…]
Scarlet macaw
[…]very few web sites that come about to become detailed below, from our point of view are undoubtedly well really worth checking out[…]
Mdma crystal
[…]always a big fan of linking to bloggers that I love but dont get lots of link love from[…]
Gun shop near me
[…]below youll find the link to some web sites that we feel you need to visit[…]
Buy Research Chemicals Online
[…]just beneath, are various completely not connected sites to ours, having said that, they may be certainly really worth going over[…]
Buy Marijuana Online
[…]The data talked about within the write-up are a number of the most effective available […]
Buy Marijuana Online
[…]always a huge fan of linking to bloggers that I really like but really don’t get a great deal of link appreciate from[…]
Movie Download Site
[…]The data talked about within the report are some of the best available […]
Juul Pod Flavors
[…]the time to study or visit the content material or sites we’ve linked to below the[…]
Mango Juul Pods
[…]although web sites we backlink to below are considerably not connected to ours, we feel they’re truly really worth a go as a result of, so possess a look[…]
https://geant.23video.com/tnc15-7a-wednesday-plenary
[…]Here is an excellent Weblog You might Discover Intriguing that we Encourage You[…]
Juul mint pods
[…]we prefer to honor many other world-wide-web websites around the internet, even if they arent linked to us, by linking to them. Underneath are some webpages worth checking out[…]
https://antcarp7.webs.com/apps/blog/show/48074671-picture-games-are-usable-for-citizenry-from-whole-accomplishment-levels-and-interests-it-lets-you-unbend-and-savor-sprightliness-sir-thomas-more-this-article-contains-advice-that-testament-aid-you-wit…
[…]Here is a good Weblog You might Discover Intriguing that we Encourage You[…]
where to buy meth
[…]check below, are some absolutely unrelated web-sites to ours, nonetheless, they’re most trustworthy sources that we use[…]
marijuana for sale
[…]Sites of interest we have a link to[…]
realistic dildo
[…]one of our visitors not too long ago recommended the following website[…]
flexible dildo
[…]Every when inside a when we decide on blogs that we read. Listed below would be the latest websites that we pick […]
THC VAPE OIL
[…]The information and facts talked about inside the write-up are some of the best offered […]
Smoke Shop Near Me Now
[…]we prefer to honor several other web sites around the web, even when they arent linked to us, by linking to them. Below are some webpages really worth checking out[…]
oxycodone 30mg for sale
[…]one of our visitors not long ago proposed the following website[…]
xanax for sale
[…]that may be the end of this report. Right here youll discover some sites that we think you will appreciate, just click the hyperlinks over[…]
buy ativanbuy lorazepam online
[…]Here is an excellent Weblog You may Find Interesting that we Encourage You[…]
Vape stores near me
[…]the time to read or visit the content material or websites we have linked to below the[…]
where to buy xanax
[…]Sites of interest we have a link to[…]
buy hydrocodone online legit
[…]that may be the end of this report. Right here you will uncover some web sites that we believe youll value, just click the links over[…]
كوتشي
[…]the time to read or go to the content or web sites we’ve linked to below the[…]
buy CBD oil
[…]we prefer to honor several other online web pages on the web, even when they arent linked to us, by linking to them. Under are some webpages really worth checking out[…]
best CBD oil for dogs
[…]just beneath, are many totally not related internet sites to ours, even so, they’re certainly really worth going over[…]
best CBD oil for sleep
[…]please pay a visit to the internet sites we stick to, such as this one, because it represents our picks from the web[…]
best CBD oil for sleep
[…]Every the moment in a even though we pick blogs that we read. Listed below are the most up-to-date sites that we pick […]
best CBD cream for arthritis pain
[…]Every after inside a when we pick out blogs that we study. Listed below would be the most current websites that we pick […]
buy CBD oil
[…]please go to the sites we follow, which includes this a single, as it represents our picks through the web[…]
best CBD oil for arthritis
[…]below you will discover the link to some web pages that we assume you’ll want to visit[…]
best CBD oil for anxiety
[…]we prefer to honor a lot of other world wide web web-sites around the net, even when they arent linked to us, by linking to them. Underneath are some webpages really worth checking out[…]
best CBD oil for pain
[…]Sites of interest we’ve a link to[…]
best CBD oil for pain
[…]Sites of interest we have a link to[…]
best CBD capsules
[…]below you will come across the link to some web pages that we believe you’ll want to visit[…]
best CBD capsules
[…]Here is a superb Weblog You might Come across Interesting that we Encourage You[…]
best CBD oil
[…]very few internet websites that occur to be in depth below, from our point of view are undoubtedly nicely really worth checking out[…]
best CBD oil
[…]always a big fan of linking to bloggers that I like but really don’t get a lot of link love from[…]
best CBD gummies
[…]Here are some of the internet sites we recommend for our visitors[…]
Buy hydrocodone online
[…]Here are some of the sites we advise for our visitors[…]
Buy Nembutal online
[…]usually posts some extremely fascinating stuff like this. If you are new to this site[…]
Buy subutex 8mg online
[…]check beneath, are some totally unrelated sites to ours, nevertheless, they are most trustworthy sources that we use[…]
Buy real Xanax online
[…]just beneath, are several absolutely not associated websites to ours, even so, they are surely worth going over[…]
free app download
[…]The data mentioned in the post are several of the ideal readily available […]
free download for laptop
[…]The facts mentioned inside the article are several of the very best accessible […]
apps download for windows 10
[…]always a massive fan of linking to bloggers that I appreciate but do not get lots of link really like from[…]
free download for pc
[…]just beneath, are quite a few absolutely not related web-sites to ours, having said that, they may be surely worth going over[…]
games free download for windows 10
[…]Wonderful story, reckoned we could combine a number of unrelated data, nevertheless definitely worth taking a appear, whoa did one particular understand about Mid East has got extra problerms too […]
pc app free download
[…]Here are some of the websites we recommend for our visitors[…]
apps download for windows 10
[…]please go to the web-sites we comply with, like this 1, as it represents our picks from the web[…]
free download for laptop pc
[…]Sites of interest we have a link to[…]
pc app free download
[…]one of our visitors lately advised the following website[…]
free pc games download
[…]Wonderful story, reckoned we could combine a few unrelated data, nevertheless seriously worth taking a search, whoa did a single study about Mid East has got more problerms also […]
Counterfeit-Money For Sale
[…]that is the end of this post. Right here you will come across some web-sites that we feel youll appreciate, just click the links over[…]
Fake Money That Looks Real Printable
[…]Here are some of the web pages we recommend for our visitors[…]
Where To Buy Xanax Online
[…]always a major fan of linking to bloggers that I really like but really don’t get a good deal of link love from[…]
Order Ambien Online
[…]Wonderful story, reckoned we could combine a couple of unrelated information, nevertheless seriously worth taking a appear, whoa did one understand about Mid East has got a lot more problerms as well […]
Best Place To Buy Vicodin Online
[…]below you will locate the link to some internet sites that we feel you must visit[…]
brand awearness strategy
[…]very couple of sites that transpire to be in depth below, from our point of view are undoubtedly well really worth checking out[…]
Dankwoods Dank Vapes
[…]we like to honor quite a few other web websites around the net, even though they arent linked to us, by linking to them. Below are some webpages really worth checking out[…]
Stoney Patch Gummies
[…]always a large fan of linking to bloggers that I like but really don’t get a great deal of link like from[…]
Freelance Jobs
[…]Here are a few of the web sites we advocate for our visitors[…]
Creation des sites web
[…]although web sites we backlink to below are considerably not connected to ours, we really feel they’re essentially really worth a go by, so have a look[…]
how to be a marketing affiliate
[…]Wonderful story, reckoned we could combine several unrelated data, nonetheless actually really worth taking a appear, whoa did one particular understand about Mid East has got far more problerms as well […]
best online email marketing course
[…]Here are a few of the websites we recommend for our visitors[…]
Download Premium WordPress Themes Free
[…]very couple of websites that take place to become in depth below, from our point of view are undoubtedly very well worth checking out[…]
Free Robux
[…]although web sites we backlink to below are considerably not related to ours, we really feel they may be basically worth a go through, so have a look[…]
Earn Free Robux Here
[…]Every when in a though we choose blogs that we study. Listed below are the newest internet sites that we decide on […]
how to win at casino
[…]although websites we backlink to below are considerably not associated to ours, we really feel they may be really worth a go as a result of, so possess a look[…]
how to win at roulette
[…]please stop by the web sites we stick to, which includes this 1, as it represents our picks from the web[…]
drone services
[…]very handful of web sites that happen to be in depth below, from our point of view are undoubtedly properly really worth checking out[…]
vape shop near me
[…]check below, are some completely unrelated websites to ours, nevertheless, they may be most trustworthy sources that we use[…]
DR. MANPREET BAJWA CBD Fraud
[…]the time to study or take a look at the content or web pages we have linked to below the[…]
Real Dank Vapes-Dank
[…]one of our visitors not long ago advised the following website[…]
CARA THIEN CBD Scammer
[…]The information mentioned in the post are several of the top accessible […]
make money online
[…]the time to read or stop by the content or web sites we have linked to beneath the[…]
Kratom Near Me
[…]please visit the sites we adhere to, like this one particular, because it represents our picks from the web[…]
win at roulette
[…]we like to honor numerous other world-wide-web web pages on the net, even though they arent linked to us, by linking to them. Below are some webpages really worth checking out[…]
buy CBD oil
[…]the time to read or pay a visit to the material or web-sites we have linked to beneath the[…]
CBD oil for arthritis
[…]Here are a number of the web sites we recommend for our visitors[…]
This is for Rachel Lyrics
[…]The details talked about within the write-up are some of the most beneficial offered […]
CBD oil for pain
[…]please check out the web-sites we stick to, such as this one particular, because it represents our picks in the web[…]
buy CBD oils
[…]the time to read or stop by the material or web pages we’ve linked to below the[…]
best CBD oils
[…]although web-sites we backlink to beneath are considerably not connected to ours, we feel they’re actually worth a go through, so have a look[…]
free instagram followers
[…]check beneath, are some absolutely unrelated sites to ours, nonetheless, they may be most trustworthy sources that we use[…]
xxx
[…]the time to read or check out the content or web pages we have linked to below the[…]
Buy Weed Online
[…]here are some hyperlinks to internet sites that we link to for the reason that we consider they’re worth visiting[…]
Vape shop Near Me
[…]we like to honor lots of other internet internet sites on the internet, even when they arent linked to us, by linking to them. Underneath are some webpages worth checking out[…]
Youtube To Song Downloader
[…]Here are some of the web pages we suggest for our visitors[…]
affiliate marketing business with amazon
[…]just beneath, are quite a few entirely not related web-sites to ours, however, they’re surely really worth going over[…]
Freemake Video Converter Key
[…]always a huge fan of linking to bloggers that I really like but dont get a whole lot of link love from[…]
amazon fba
[…]one of our visitors a short while ago advised the following website[…]
how to get started with affiliate marketing
[…]The facts mentioned in the post are some of the most effective out there […]
how to be a affiliate marketer
[…]please take a look at the web-sites we stick to, including this one particular, because it represents our picks through the web[…]
Movavi Video Converter Activation Key
[…]that would be the end of this report. Here youll obtain some web-sites that we assume youll value, just click the hyperlinks over[…]
Research chemicals for sale
[…]please visit the web-sites we follow, which includes this one particular, because it represents our picks through the web[…]
Best Cleaning Company in Abu Dhabi
[…]although sites we backlink to below are considerably not associated to ours, we really feel they are actually really worth a go through, so have a look[…]
websites for sale
[…]always a large fan of linking to bloggers that I love but dont get a great deal of link adore from[…]
Diazepam for sale
[…]check beneath, are some absolutely unrelated sites to ours, having said that, they may be most trustworthy sources that we use[…]
ΚΑΖΙΝΟ ΑΘΗΝΑ
[…]usually posts some quite exciting stuff like this. If you are new to this site[…]
akurat
[…]check below, are some absolutely unrelated web sites to ours, however, they may be most trustworthy sources that we use[…]
Earn Money Online
[…]always a large fan of linking to bloggers that I adore but do not get a whole lot of link like from[…]
Earn Money Online
[…]we came across a cool internet site that you may well love. Take a search for those who want[…]
Make Money Fast
[…]just beneath, are numerous absolutely not related web sites to ours, having said that, they are surely really worth going over[…]
Make Money Fast
[…]although internet sites we backlink to below are considerably not connected to ours, we really feel they are in fact worth a go via, so have a look[…]
Work from Home Jobs
[…]usually posts some very exciting stuff like this. If youre new to this site[…]
Work from Home Jobs
[…]below youll find the link to some web pages that we assume you must visit[…]
Silicone Baking Mats
[…]here are some hyperlinks to web-sites that we link to mainly because we think they’re worth visiting[…]
Silicone Baking Mats
[…]Every the moment inside a even though we pick out blogs that we study. Listed beneath would be the most current sites that we select […]
free robux hack
[…]Wonderful story, reckoned we could combine a handful of unrelated data, nonetheless actually worth taking a look, whoa did a single study about Mid East has got much more problerms at the same time […]
Make Money Fast
[…]Here are several of the web sites we recommend for our visitors[…]
OnHaxx
[…]we like to honor several other net internet sites on the internet, even when they arent linked to us, by linking to them. Underneath are some webpages really worth checking out[…]
OnHax
[…]Here is a superb Weblog You may Come across Interesting that we Encourage You[…]
OnHaxx
[…]usually posts some quite exciting stuff like this. If you are new to this site[…]
Gelato Strain
[…]very couple of internet sites that come about to be in depth below, from our point of view are undoubtedly effectively really worth checking out[…]
free app for pc download
[…]just beneath, are various entirely not connected web pages to ours, even so, they may be certainly worth going over[…]
app pc download for windows
[…]check beneath, are some absolutely unrelated websites to ours, however, they may be most trustworthy sources that we use[…]
pc games for windows 8
[…]Wonderful story, reckoned we could combine several unrelated data, nonetheless definitely really worth taking a appear, whoa did 1 discover about Mid East has got a lot more problerms too […]
tko carts
[…]usually posts some extremely fascinating stuff like this. If youre new to this site[…]
Cookies Carts
[…]below youll find the link to some sites that we think you’ll want to visit[…]
Purchase Weed Online
[…]below you will obtain the link to some web-sites that we believe it is best to visit[…]
kratom online
[…]we came across a cool web-site which you may possibly appreciate. Take a appear when you want[…]
Kratom Near Me
[…]check below, are some absolutely unrelated web sites to ours, however, they’re most trustworthy sources that we use[…]
Marijuana Strains
[…]Here is a superb Weblog You may Find Interesting that we Encourage You[…]
Disposable Vape
[…]one of our guests lately recommended the following website[…]
Movie Download Site
[…]we came across a cool internet site that you just may well love. Take a look in the event you want[…]
OnHaxx
[…]The details mentioned within the report are a few of the most effective offered […]
смотреть перейдя сюда VIDEO.info
[…]check below, are some completely unrelated web sites to ours, however, they may be most trustworthy sources that we use[…]
Buy Weed Online
[…]we came across a cool site that you might enjoy. Take a appear should you want[…]
Dank Vapes
[…]Wonderful story, reckoned we could combine a couple of unrelated data, nonetheless genuinely worth taking a appear, whoa did a single find out about Mid East has got extra problerms as well […]
Jed Fernandez
[…]although web sites we backlink to below are considerably not related to ours, we feel they’re essentially worth a go through, so possess a look[…]
e-library
[…]below you will discover the link to some websites that we assume you should visit[…]
e-library
[…]we came across a cool web page that you simply might take pleasure in. Take a look in case you want[…]
ed pills that work
Listening Room Acoustics: Room Modes and Standing Waves – NOVO Audio and Technology Magazine
free pc games download
[…]very handful of sites that take place to be in depth below, from our point of view are undoubtedly very well worth checking out[…]
buy or sell ads
[…]one of our guests recently proposed the following website[…]
birman kittens for sale
[…]the time to read or visit the subject material or web pages we’ve linked to beneath the[…]
cebeci profilo servisi
[…]the time to read or visit the material or web pages we’ve linked to beneath the[…]
servisi/ cevizlidere profilo servisi
[…]although internet websites we backlink to below are considerably not connected to ours, we feel they are really worth a go via, so possess a look[…]
Ayurveda Online Shop
[…]the time to read or take a look at the content material or websites we have linked to below the[…]
Sonia Randhawa
[…]the time to study or visit the content material or web-sites we’ve linked to below the[…]
Order 100mg Tramadol Online
[…]always a huge fan of linking to bloggers that I enjoy but really don’t get lots of link like from[…]
kratom near me
[…]although web-sites we backlink to below are considerably not connected to ours, we really feel they’re basically really worth a go as a result of, so have a look[…]
Amsterdam escorts
[…]The information and facts mentioned inside the report are some of the most beneficial offered […]
710 king pen
[…]below you will locate the link to some internet sites that we consider you ought to visit[…]
Buy Weed Online
[…]Here is a superb Blog You may Find Intriguing that we Encourage You[…]
Sonia Randhawa
[…]Wonderful story, reckoned we could combine several unrelated information, nevertheless actually really worth taking a search, whoa did 1 learn about Mid East has got far more problerms as well […]
fake money for sale
[…]Here is a good Weblog You may Obtain Intriguing that we Encourage You[…]
search engine optimization hong kong
[…]the time to study or go to the subject material or sites we’ve linked to below the[…]
Brass Knuckles Vape
[…]below you will uncover the link to some sites that we consider you need to visit[…]
Kingpen
[…]Sites of interest we’ve a link to[…]
Kingpen
[…]Wonderful story, reckoned we could combine a few unrelated data, nevertheless actually worth taking a search, whoa did one discover about Mid East has got much more problerms also […]
seattle commercial pest control service
[…]that could be the finish of this article. Right here you will obtain some internet sites that we assume you will appreciate, just click the links over[…]
book store near me
[…]that may be the end of this post. Right here you will come across some sites that we think you will appreciate, just click the hyperlinks over[…]
5euros
[…]usually posts some extremely intriguing stuff like this. If you are new to this site[…]
buy careprost in the usa
Listening Room Acoustics: Room Modes and Standing Waves – NOVO Audio and Technology Magazine
زن شوهردار به یه پسر حشری کوس میده
[…]we came across a cool internet site which you may possibly delight in. Take a look when you want[…]
Reverse telephone directory
[…]that could be the end of this post. Here you will obtain some web pages that we assume youll value, just click the links over[…]
big black cock enter’s rajapandi’s tender asshole
[…]please take a look at the sites we adhere to, like this one particular, as it represents our picks in the web[…]
buy viagra professional
Listening Room Acoustics: Room Modes and Standing Waves – NOVO Audio and Technology Magazine
عزة وثقة
[…]Every after in a though we opt for blogs that we read. Listed below would be the latest sites that we opt for […]
الم
[…]Sites of interest we’ve a link to[…]
RoyalCBD.com
[…]Every the moment in a though we decide on blogs that we read. Listed below are the most current web-sites that we choose […]
terpenes
[…]Sites of interest we’ve a link to[…]
RoyalCBD.com
[…]Every when in a whilst we select blogs that we read. Listed below are the most up-to-date web-sites that we decide on […]
Royal CBD
[…]that will be the finish of this article. Here youll obtain some websites that we assume youll enjoy, just click the hyperlinks over[…]
https://royalcbd.com/can-you-overdose-on-cbd/
[…]very handful of websites that come about to be detailed below, from our point of view are undoubtedly very well really worth checking out[…]
buy hydroxychloroquine online
Listening Room Acoustics: Room Modes and Standing Waves – NOVO Audio and Technology Magazine
RoyalCBD
[…]Wonderful story, reckoned we could combine a few unrelated information, nonetheless definitely worth taking a search, whoa did a single learn about Mid East has got additional problerms too […]
RoyalCBD.com
[…]please pay a visit to the web sites we follow, including this a single, as it represents our picks through the web[…]
virginia cbd
[…]The facts talked about within the article are some of the best readily available […]
cbd oil oklahoma
[…]we prefer to honor numerous other web sites around the web, even when they arent linked to us, by linking to them. Beneath are some webpages worth checking out[…]
RoyalCBD.com
[…]Sites of interest we have a link to[…]
RoyalCBD.com
[…]The info talked about inside the write-up are several of the most beneficial accessible […]
RoyalCBD.com
[…]check below, are some entirely unrelated web-sites to ours, nonetheless, they’re most trustworthy sources that we use[…]
is cbd legal in new jersey
[…]please visit the sites we stick to, like this a single, as it represents our picks through the web[…]
Royal CBD
[…]below you will locate the link to some sites that we feel it is best to visit[…]
cbd michigan
[…]Here are a few of the web-sites we suggest for our visitors[…]
minnesota cbd
[…]that will be the end of this post. Here you will discover some web sites that we assume you will appreciate, just click the hyperlinks over[…]
Royal CBD
[…]Here is an excellent Blog You may Find Interesting that we Encourage You[…]
https://royalcbd.com/illinois/
[…]Here are a number of the sites we advocate for our visitors[…]
Royal CBD
[…]the time to read or go to the material or sites we have linked to beneath the[…]
cbd oil arkansas
[…]Wonderful story, reckoned we could combine a few unrelated data, nevertheless definitely really worth taking a search, whoa did 1 study about Mid East has got much more problerms as well […]
alaska cbd
[…]very few internet websites that take place to be in depth below, from our point of view are undoubtedly well worth checking out[…]
RoyalCBD.com
[…]Every once inside a although we decide on blogs that we study. Listed beneath would be the newest internet sites that we choose […]
RoyalCBD.com
[…]always a huge fan of linking to bloggers that I enjoy but dont get a good deal of link really like from[…]
RoyalCBD
[…]please take a look at the sites we adhere to, such as this one, because it represents our picks from the web[…]
https://royalcbd.com/cbd-oil-side-effects/
[…]we prefer to honor many other web websites around the internet, even if they arent linked to us, by linking to them. Below are some webpages really worth checking out[…]
RoyalCBD.com
[…]Every as soon as inside a although we decide on blogs that we read. Listed below are the newest internet sites that we opt for […]
cbd legal status
[…]although internet websites we backlink to beneath are considerably not associated to ours, we really feel they may be essentially worth a go through, so have a look[…]
m sucht m
[…]here are some links to web-sites that we link to because we assume they’re worth visiting[…]
MALWAREBYTES LOGIN
[…]we prefer to honor lots of other web websites on the web, even if they arent linked to us, by linking to them. Under are some webpages really worth checking out[…]
investment sales broker
[…]very few sites that transpire to become comprehensive below, from our point of view are undoubtedly very well really worth checking out[…]
Electrician SEO
[…]the time to study or take a look at the content or web sites we’ve linked to beneath the[…]
free windows app download
[…]usually posts some extremely interesting stuff like this. If you are new to this site[…]
Laptop support
[…]usually posts some quite interesting stuff like this. If you are new to this site[…]
Cavapoo Puppies for sale
[…]usually posts some quite exciting stuff like this. If you are new to this site[…]
Teacup Puppies For Sale
[…]always a big fan of linking to bloggers that I love but really don’t get a whole lot of link really like from[…]
Escorts amsterdam
[…]that may be the end of this write-up. Here youll locate some websites that we feel you will value, just click the hyperlinks over[…]
long sleeve velvet bodysuit
[…]that is the end of this post. Right here youll uncover some web-sites that we feel youll enjoy, just click the links over[…]
mksorb.com
[…]we prefer to honor quite a few other world wide web websites around the net, even if they arent linked to us, by linking to them. Under are some webpages worth checking out[…]
سکس با مشتری
[…]Sites of interest we have a link to[…]
doberman pinscher
[…]just beneath, are many completely not related sites to ours, having said that, they’re surely really worth going over[…]
counterfeit money for sale 2019
[…]here are some hyperlinks to internet sites that we link to simply because we assume they may be worth visiting[…]
Buy Cocaine Online
[…]below you will locate the link to some web pages that we believe you must visit[…]
order fake money online
[…]usually posts some quite intriguing stuff like this. If you are new to this site[…]
Venice photography
[…]one of our guests lately proposed the following website[…]
STUDY IN AUSTRALIA FOR INDIAN STUDENTS
[…]check below, are some totally unrelated web-sites to ours, nonetheless, they are most trustworthy sources that we use[…]
free download for windows 8
[…]Sites of interest we’ve a link to[…]
Employee health insurance plans
[…]we came across a cool website which you may possibly enjoy. Take a look when you want[…]
Employee benefits
[…]here are some links to sites that we link to mainly because we consider they are really worth visiting[…]
physio für hunde
[…]please take a look at the web sites we comply with, which includes this a single, because it represents our picks in the web[…]
russian fairy tales book
[…]The data mentioned within the post are several of the very best available […]
wolfbet
[…]Sites of interest we have a link to[…]
stake
[…]very handful of internet websites that come about to become detailed below, from our point of view are undoubtedly properly worth checking out[…]
Prof. Eucharia Kenya
[…]The info talked about inside the article are several of the ideal offered […]
Visa
[…]please visit the web sites we comply with, like this one, as it represents our picks through the web[…]
exchange crypto
[…]Sites of interest we have a link to[…]
Top Shelf Electric Heating & Air
[…]below you will find the link to some websites that we feel you ought to visit[…]
colorado web impressions
[…]usually posts some extremely intriguing stuff like this. If you are new to this site[…]
IT Recycling newbury
[…]just beneath, are quite a few completely not associated websites to ours, nevertheless, they may be certainly really worth going over[…]
Obesity Surgery in Turkey
[…]that is the finish of this article. Right here you will uncover some web pages that we believe you will value, just click the hyperlinks over[…]
pubg lite hile satın al
[…]we came across a cool web page that you just may possibly get pleasure from. Take a look if you want[…]
Maine Coon Kittens For Sale Near Me
[…]Sites of interest we have a link to[…]
kittens for adoption
[…]below you will find the link to some web-sites that we believe you ought to visit[…]
small vibrating dildo
[…]always a major fan of linking to bloggers that I really like but dont get a whole lot of link appreciate from[…]
thy uçak bileti
[…]the time to study or pay a visit to the content material or web sites we’ve linked to below the[…]
macca
[…]The information and facts talked about within the post are some of the ideal accessible […]
giayu2
[…]although internet sites we backlink to beneath are considerably not related to ours, we really feel they’re actually really worth a go by, so have a look[…]
sex education
[…]Here is a superb Blog You might Find Intriguing that we Encourage You[…]
blogcaodep.com
[…]Here is a superb Blog You might Discover Interesting that we Encourage You[…]
visit their website panos germanos
[…]Here are a few of the websites we suggest for our visitors[…]
Damiana
[…]here are some links to web-sites that we link to mainly because we consider they may be worth visiting[…]
wasmachine monteur
[…]Wonderful story, reckoned we could combine a handful of unrelated data, nevertheless truly worth taking a look, whoa did one master about Mid East has got far more problerms at the same time […]
tabakvervanger
[…]we came across a cool web site that you simply may possibly enjoy. Take a look when you want[…]
solar system companies in pakistan
[…]check beneath, are some completely unrelated internet sites to ours, even so, they’re most trustworthy sources that we use[…]
Bluetooth with headphones
[…]we like to honor several other net web-sites on the internet, even if they arent linked to us, by linking to them. Below are some webpages worth checking out[…]
where to buy Mini Australian Shepherds
[…]although internet websites we backlink to beneath are considerably not associated to ours, we feel they may be in fact worth a go by, so possess a look[…]
sývý klor
[…]we came across a cool web page that you could love. Take a appear if you want[…]
havuz kimyasallarý
[…]we like to honor numerous other world wide web websites on the net, even though they arent linked to us, by linking to them. Underneath are some webpages really worth checking out[…]
mobilya
[…]Sites of interest we have a link to[…]
resource ΑΠΟΦΡΑΞΕΙΣ
[…]Every as soon as in a when we choose blogs that we study. Listed below would be the newest sites that we choose […]
how to choose kamado grill
[…]we like to honor many other world-wide-web web-sites on the internet, even though they arent linked to us, by linking to them. Beneath are some webpages worth checking out[…]
German shepherd puppies for sale Near Me
[…]check beneath, are some totally unrelated sites to ours, having said that, they are most trustworthy sources that we use[…]
Gun Shops Near Me
[…]the time to study or stop by the content material or internet sites we have linked to beneath the[…]
Buy cocaine online
[…]usually posts some really interesting stuff like this. If you are new to this site[…]
Psilocybe baeocystis
[…]one of our visitors recently proposed the following website[…]
Magic Mush Rooms
[…]The facts mentioned in the write-up are some of the best accessible […]
Puppies for adoption near me
[…]the time to study or go to the subject material or websites we have linked to beneath the[…]
THC VAPE JUICE
[…]one of our guests not too long ago suggested the following website[…]
blue nose pitbull puppies for sale
[…]The data talked about inside the report are several of the best accessible […]
hardcore sex videos
[…]please pay a visit to the web pages we adhere to, such as this a single, as it represents our picks through the web[…]
Gulberg Greens
[…]one of our guests not too long ago advised the following website[…]